题目内容
1.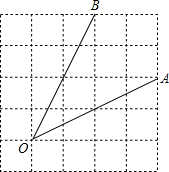 如图.∠AOB在格点图中,则sin∠AOB的值为( )
如图.∠AOB在格点图中,则sin∠AOB的值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{3}{5}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
分析 连接AB,过A作AD⊥OB,易求△AOB的面积,根据勾股定理可求出OA,OB的长,进而可求出AD的长,根据正弦的定义计算即可.
解答 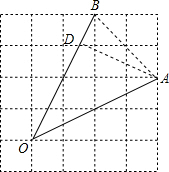 解:如图,连接AB,过A作AD⊥OB,
解:如图,连接AB,过A作AD⊥OB,
设每个小正方形边长为1,
∵S△AOB=4×4-2×4-$\frac{1}{2}$×2×2=6,
由勾股定理可得:OB=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,OA=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∴AD=$\frac{12}{OB}$=$\frac{6\sqrt{5}}{5}$,
∴∠AOB的正弦值=$\frac{AD}{OA}$=$\frac{3}{5}$,
故选B.
点评 考查了勾股定理,本题主要通过构造直角三角形,利用勾股定理和锐角三角函数的定义求解的,

练习册系列答案
相关题目
12.小明从家里出发到学校共经过3个路口,每个路口都有红绿灯,如果红灯亮的时间为20秒,绿灯亮的时间为40秒,那么小明从家里出发到学校一路通行无阻的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{8}{27}$ | D. | $\frac{2}{9}$ |
6.下列各式计算正确的是( )
| A. | (a+b)2=a2+b2 | B. | a•a2=a3 | C. | a8÷a2=a4 | D. | 3a2+2a2=5a4 |
10.下列说法中错误的是( )
| A. | 5y4是四次单项式 | B. | 2a3-3ab2+5b3是三次三项式 | ||
| C. | $\frac{{a}^{2}{b}^{4}}{3}$的系数是3 | D. | 0是单项式 |
11.有一组数据如下:3,a,4,6,7,它们的平均数是5,那么这组数据的方差是( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{10}$ | D. | 10 |