题目内容
 如图,在△ABC中,∠BAC=100°,点D、E在BC上,且BA=BE,CA=CD,则∠DAE等于( )
如图,在△ABC中,∠BAC=100°,点D、E在BC上,且BA=BE,CA=CD,则∠DAE等于( )| A、30° | B、35° |
| C、40° | D、45° |
考点:等腰三角形的性质
专题:
分析:根据等腰三角形性质得出∠BAE=∠BEA,∠CAD=∠CDA,根据三角形内角和定理得出∠B=180°-2∠BAE①,∠C=180°-2∠CAD②,①+②得出∠B+∠C=360°-2(∠BAE+∠CAD),求出2∠DAE=180°-∠BAC,代入求出即可.
解答:解:∵BE=BA,
∴∠BAE=∠BEA,
∴∠B=180°-2∠BAE,①
∵CD=CA,
∴∠CAD=∠CDA,
∴∠C=180°-2∠CAD,②
①+②得:∠B+∠C=360°-2(∠BAE+∠CAD)
∴180°-∠BAC=360°-2[(∠BAD+∠DAE)+(∠DAE+∠CAE)],
∴-∠BAC=180°-2[(∠BAD+∠DAE+∠CAD)+∠DAE],
∴-∠BAC=180°-2(∠BAC+∠DAE),
∴2∠DAE=180°-∠BAC.
∵∠BAC=100°,
∴2∠DAE=180°-100°=80°,
∴∠DAE=40°,
故选C.
∴∠BAE=∠BEA,
∴∠B=180°-2∠BAE,①
∵CD=CA,
∴∠CAD=∠CDA,
∴∠C=180°-2∠CAD,②
①+②得:∠B+∠C=360°-2(∠BAE+∠CAD)
∴180°-∠BAC=360°-2[(∠BAD+∠DAE)+(∠DAE+∠CAE)],
∴-∠BAC=180°-2[(∠BAD+∠DAE+∠CAD)+∠DAE],
∴-∠BAC=180°-2(∠BAC+∠DAE),
∴2∠DAE=180°-∠BAC.
∵∠BAC=100°,
∴2∠DAE=180°-100°=80°,
∴∠DAE=40°,
故选C.
点评:本题考查了三角形内角和定理,等腰三角形的性质的应用,关键是推出2∠DAE=180°-∠BAC.

练习册系列答案
相关题目
已知△ABC的三边分别是a,b,c,两圆的半径r1=a,r2=b,圆心距d=c,则这两个圆的位置关系是( )
| A、相交 | B、外切 | C、内切 | D、相离 |
 已知P(a,b)是第一象限内的矩形ABCD(含边界)中的一个动点,A、B、C、D的坐标如图所示,则
已知P(a,b)是第一象限内的矩形ABCD(含边界)中的一个动点,A、B、C、D的坐标如图所示,则| b |
| a |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在△ABC中,点D是AC上一点,且AB2=AD•AC,AE平分∠BAC交BD于点E,过E作EF∥AC交BC于点F,若BE=5,则CF的长为
如图,在△ABC中,点D是AC上一点,且AB2=AD•AC,AE平分∠BAC交BD于点E,过E作EF∥AC交BC于点F,若BE=5,则CF的长为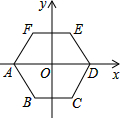 如图,将正六边形ABCDEF放在直角坐标系中,其中心与坐标原点重合,若A点的坐标为(-
如图,将正六边形ABCDEF放在直角坐标系中,其中心与坐标原点重合,若A点的坐标为(- 如图,一正方形的棱长为2,一只蚂蚁在顶点A处,在顶点G处有一米粒.
如图,一正方形的棱长为2,一只蚂蚁在顶点A处,在顶点G处有一米粒. 如图,点D、E分别在线段AB,AC上,AE=AD,不添加新的线段和字母,要使△ABE≌△ACD,需添加的一个条件是
如图,点D、E分别在线段AB,AC上,AE=AD,不添加新的线段和字母,要使△ABE≌△ACD,需添加的一个条件是