题目内容
 如图,在△ABC中,点D是AC上一点,且AB2=AD•AC,AE平分∠BAC交BD于点E,过E作EF∥AC交BC于点F,若BE=5,则CF的长为
如图,在△ABC中,点D是AC上一点,且AB2=AD•AC,AE平分∠BAC交BD于点E,过E作EF∥AC交BC于点F,若BE=5,则CF的长为考点:相似三角形的判定与性质
专题:压轴题
分析:如图作辅助线:过点E作EM⊥AB于M,作EG⊥AC于G,过点F作FN于N.则由角平分线的性质证得ME=GE;根据平行四边形的判定得到四边形EGNF是平行四边形,所以GE=NF.通过证明△BEM≌△CFN得到CF=BE.
解答: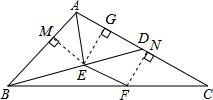 解:如图,过点E作EM⊥AB于M,作EG⊥AC于G,过点F作FN⊥AC于N,则EG∥FN,
解:如图,过点E作EM⊥AB于M,作EG⊥AC于G,过点F作FN⊥AC于N,则EG∥FN,
∵AE平分∠BAC,EF∥AC
∴ME=GE,四边形EGNF是平行四边形,
∴GE=NF,
∴ME=NF.
又∵AB2=AD•AC,
∴
=
,
∵∠BAD=∠CAB,
∴△ABD∽△ACB,
∴∠ABD=∠ACB,即∠MBE=∠NCF,
∴在△BEM与△CFN中,
,
∴△BEM≌△CFN(AAS),
∴CF=BE=5.
故填:5.
 解:如图,过点E作EM⊥AB于M,作EG⊥AC于G,过点F作FN⊥AC于N,则EG∥FN,
解:如图,过点E作EM⊥AB于M,作EG⊥AC于G,过点F作FN⊥AC于N,则EG∥FN,∵AE平分∠BAC,EF∥AC
∴ME=GE,四边形EGNF是平行四边形,
∴GE=NF,
∴ME=NF.
又∵AB2=AD•AC,
∴
| AB |
| AC |
| AD |
| AB |
∵∠BAD=∠CAB,
∴△ABD∽△ACB,
∴∠ABD=∠ACB,即∠MBE=∠NCF,
∴在△BEM与△CFN中,
|
∴△BEM≌△CFN(AAS),
∴CF=BE=5.
故填:5.
点评:本题考查了相似三角形的判定与性质.在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件.

练习册系列答案
相关题目
 如图,在△ABC中,∠BAC=100°,点D、E在BC上,且BA=BE,CA=CD,则∠DAE等于( )
如图,在△ABC中,∠BAC=100°,点D、E在BC上,且BA=BE,CA=CD,则∠DAE等于( )| A、30° | B、35° |
| C、40° | D、45° |
 某同学按照如下步骤操作:
某同学按照如下步骤操作: 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:其中所有正确结论的序号是
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:其中所有正确结论的序号是 如图,已知反比例函数y=
如图,已知反比例函数y=