题目内容

把二次函数y=x2-2x+4化成顶点式为（　　）
A、y=（x-1）2+2
B、y=（x+1）2+3
C、y=（x-1）2
D、y=（x-1）2+3
考点：二次函数的三种形式
专题：
分析：根据配方法的操作整理即可得解．
解答：解：y=x2-2x+4，
=x2-2x+1+3，
=（x-1）2+3．
故选D．
点评：本题考查了二次函数的三种形式，熟练掌握配方法的操作是解题的关键．
练习册系列答案
相关题目
因式分解：x2-1=
 
．
下列等式成立的是（　　）
A、
9
-
4
=
5
B、
5
×
3
=
15
C、
32+42
=7
D、-
(-3)2
=3
已知三角形内的一个点到它的三边距离相等，那么这个点是（　　）
A、三角形的外心
B、三角形的重心
C、三角形的内心
D、三角形的垂心
下列各式：
①（-7）+（-7）=0；②（-3）2=-9；③（-2）3=-6；④-33=-27；⑤
22
3
=
4
9
．
其中运算正确的有（　　）
A、0个B、1个C、2个D、3个
已知|x|=3，y2=4且x＜y，则xy的值等于（　　）
A、6B、-6
C、6或-6D、以上答案都不对
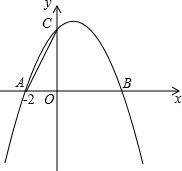如图，已知抛物线y=ax2+bx+4与x轴交于A（-2，0）、B两点，与y轴交于C点，其对称轴为直线x=1．
（1）直接写出抛物线的解析式：
 
；
（2）把线段AC沿x轴向右平移，设平移后A、C的对应点分别为A′、C′，当C′落在抛物线上时，求A′、C′的坐标；
（3）除（2）中的点A′、C′外，在x轴和抛物线上是否还分别存在点E、F，使得以A、C、E、F为顶点的四边形为平行四边形？若存在，求出E、F的坐标；若不存在，请说明理由．
如图，已知正比例函数y=ax与反比例函数y=
k
x
（k＞0）的图象交于A、B两点．且点A的坐标为（4，2）．
（1）求a、k的值；
（2）若双曲线y=
k
x
（k＞0）在第一象限的一支上存在一点C，且△AOC的面积为15，求C点的坐标．
如图1，已知抛物线C1：y=x2-2x+c和直线l：y=-2x+8，直线y=kx（k＞0）与抛物线C1交于两不同点A、B，与直线l交于点P．且当k=2时，直线y=kx（k＞0）与抛物线C1只有一个交点．
（1）求c的值；
（2）求证：
1
OA
+
1
OB
=
2
OP
，并说明k满足的条件；
（3）将抛物线C1沿第一象限夹角平分线的方向平移
2
t（t＞0）个单位，再沿y轴负方向平移（t2-t）个单位得到抛物线C2，设抛物线C1和抛物线C2交于点R；如图2．
①求证无论t为何值，抛物线C2必过定点，并判断该定点与抛物线C1的位置关系；
②设点R关于直线y=1的对称点Q，抛物线C1和抛物线C2的顶点分别为点M、N，若∠MQN=90°，求此时t的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网