题目内容
20.已知等腰△ABC,AB=AC,点D为BC的中点,点E、F、P分别在射线AB,射线AC,射线AD上.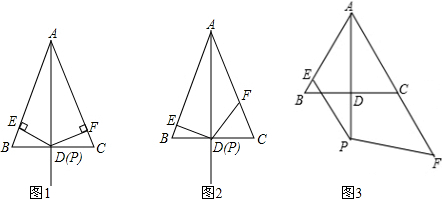
(1)如图1,当点P与点D重合时,PE⊥AB,PF⊥AC,证明:PE=PF;
(2)如图2,当点P与点D重合时,∠EPF+∠BAC=180°,(1)中的结论能否成立?若成立,请说明理由
(3)如图3,当点P在AD延长线上时,∠EPF+∠BAC=180°,(1)中的结论能否成立?若成立,请说明理由.
分析 (1)根据等腰三角形的性质,可得出AD为角平分线,再由角平分线的性质即可得出PE=PF;
(2)在AB上取点G,使AG=AF,连接DG,由等腰三角形的性质证明△AGD≌△AFD就可以得出结论;
(3)在AC上取点G,使AG=AE,连接PG,由等腰三角形的性质证明△AEP≌△AGP就可以得出结论.
解答  解:(1)∵AB=AC,点D为BC的中点,
解:(1)∵AB=AC,点D为BC的中点,
∴∠BAD=∠CAD.
∵PE⊥AB,PF⊥AC,
∴PE=PF;
(2)在AB上取点G,使AG=AF,连接DG,如图1,
∵AB=AC,点D为BC的中点,
∴∠BAD=∠CAD.
在△AGD和△AFD中,
$\left\{\begin{array}{l}{AG=AF}\\{∠BAD=∠CAD}\\{AD=AD}\end{array}\right.$,
∴△AGD≌△AFD(SAS),
∴GD=FD,∠AGD=∠AFD.
∵∠BAC+∠AED+∠EDF+∠AFD=360°,且∠EPF+∠BAC=180°,
∴∠AED+∠AFD=180°,
∴∠AED+∠AGD=180°.
∵∠AGD+∠EGD=180°,
∴∠AED=∠EGD,
∴ED=GD,
∴EP=FP;
(3)EP=FP成立
理由:在AC上取点G,使AG=AE,连接PG,如图2,
∵AB=AC,点D为BC的中点,
∴∠BAD=∠CAD.
在△AEP和△AGP中,
$\left\{\begin{array}{l}{AE=AG}\\{∠BAD=∠CAD}\\{AP=AP}\end{array}\right.$,
∴△AEP≌△AGP(SAS),
∴EP=GP,∠AEP=∠AGP.
∵∠BAC+∠AEP+∠EPF+∠AFP=360°,且∠EPF+∠BAC=180°,
∴∠AEP+∠AFP=180°,
∴∠AGP+∠AFP=180°.
∵∠AGP+∠FGP=180°,
∴∠AFP=∠EGP,
∴PG=PF,
∴EP=FP.
点评 本题考查了等腰三角形的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案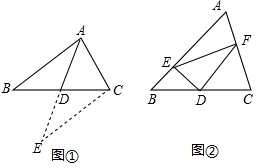 阅读下面一段对话,回答对话后面的问题:
阅读下面一段对话,回答对话后面的问题: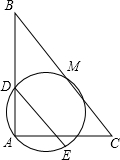 已知,如图所示,在△ABC中,∠BAC=90°,M是BC的中点,过点A、M的圆交AB于点D,过点D作DE∥BC交圆于点E,求证:DE=$\frac{1}{2}BC$.
已知,如图所示,在△ABC中,∠BAC=90°,M是BC的中点,过点A、M的圆交AB于点D,过点D作DE∥BC交圆于点E,求证:DE=$\frac{1}{2}BC$.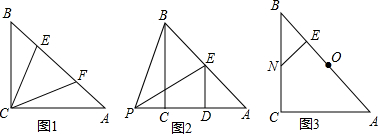
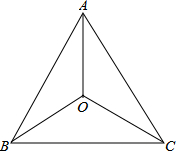 如图所示,已知OA平分∠BAC,0B=OC,求证:AB=AC.
如图所示,已知OA平分∠BAC,0B=OC,求证:AB=AC.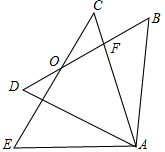 如图,AB=AC,AD=AE,BD=CE,BD与CE相交于点O,求证:∠CAB=∠EAD=∠BOC.
如图,AB=AC,AD=AE,BD=CE,BD与CE相交于点O,求证:∠CAB=∠EAD=∠BOC.