题目内容
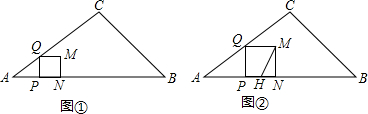
3.如图①,在△ABC中,AB=7,tanA=$\frac{3}{4}$,∠B=45°.点P从点A出发,沿AB方向以每秒1个单位长度的速度向终点B运动(不与点A、B重合),过点P作PQ⊥AB.交折线AC-CB于点Q,以PQ为边向右作正方形PQMN,设点P的运动时间为t(秒),正方形PQMN与△ABC重叠部分图形的面积为S(平方单位).(1)直接写出正方形PQMN的边PQ的长(用含t的代数式表示).
(2)当点M落在边BC上时,求t的值.
(3)求S与t之间的函数关系式.
(4)如图②,点P运动的同时,点H从点B出发,沿B-A-B的方向做一次往返运动,在B-A上的速度为每秒2个单位长度,在A-B上的速度为每秒4个单位长度,当点H停止运动时,点P也随之停止,连结MH.设MH将正方形PQMN分成的两部分图形面积分别为S1、S2(平方单位)(0<S1<S2),直接写出当S2≥3S1时t的取值范围.
分析 (1)分两种情况讨论:当点Q在线段AC上时,当点Q在线段BC上时.
(2)根据AP+PN+NB=AB,列出关于t的方程即可解答;
(3)当0<t≤$\frac{14}{5}$时,当$\frac{14}{5}$<t≤4,当4<t<7时;
(4)$\frac{28}{15}<t≤\frac{56}{27}$或$\frac{28}{9}≤t≤\frac{56}{15}$或$5≤t<\frac{21}{4}$.
解答 解:(1)当点Q在线段AC上时,PQ=tanA•AP=$\frac{3}{4}$t.
当点Q在线段BC上时,PQ=7-t.
(2)当点M落在边BC上时,如图③,
由题意得:t+$\frac{3}{4}$t$+\frac{3}{4}$t=7,
解得:t=$\frac{14}{5}$.
∴当点M落在边BC上时,求t的值为$\frac{14}{5}$.
(3)当0<t≤$\frac{14}{5}$时,如图④,
S=$(\frac{3}{4}t)^{2}$=$\frac{9}{16}{t}^{2}$.
当$\frac{14}{5}$<t≤4,如图⑤,
$S=\frac{9}{16}{t}^{2}-\frac{1}{2}(\frac{5}{2}t-7)^{2}$=$-\frac{41}{16}{t}^{2}+\frac{35}{2}t-\frac{49}{2}$.
当4<t<7时,如图⑥,
$S=\frac{1}{2}(7-t)^{2}=\frac{1}{2}{t}^{2}-7t+\frac{49}{2}$.
(4)$\frac{28}{15}<t≤\frac{56}{27}$或$\frac{28}{9}≤t≤\frac{56}{15}$或$5≤t<\frac{21}{4}$.
点评 本题正方形的性质,属于四边形综合题,解决本题的关键是进行分类讨论思想.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案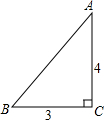 如图,一张三角形纸片ABC,其中∠C=90°,AC=4,BC=3.现小林将纸片做三次折叠:第一次使点A落在C处;将纸片展平做第二次折叠,使点B落在C处;再将纸片展平做第三次折叠,使点A落在B处.这三次折叠的折痕长依次记为a,b,c,则a,b,c的大小关系是( )
如图,一张三角形纸片ABC,其中∠C=90°,AC=4,BC=3.现小林将纸片做三次折叠:第一次使点A落在C处;将纸片展平做第二次折叠,使点B落在C处;再将纸片展平做第三次折叠,使点A落在B处.这三次折叠的折痕长依次记为a,b,c,则a,b,c的大小关系是( )| A. | c>a>b | B. | b>a>c | C. | c>b>a | D. | b>c>a |
 如图,已知四边形ABEC内接于⊙O,点D在AC的延长线上,CE平分∠BCD交⊙O于点E,则下列结论中一定正确的是( )
如图,已知四边形ABEC内接于⊙O,点D在AC的延长线上,CE平分∠BCD交⊙O于点E,则下列结论中一定正确的是( )| A. | AB=AE | B. | AB=BE | C. | AE=BE | D. | AB=AC |
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
 如图所示,数轴上点A所表示的数的相反数是2.
如图所示,数轴上点A所表示的数的相反数是2. 如图,在平行四边形ABCD中,AB=4,BC=8,∠B=60°,过平行四边形的对称中心点O的一条直线与边AD、BC分别交于点E、F,设直线EF与BC的夹角为α(如图)
如图,在平行四边形ABCD中,AB=4,BC=8,∠B=60°,过平行四边形的对称中心点O的一条直线与边AD、BC分别交于点E、F,设直线EF与BC的夹角为α(如图)