题目内容
 如图,在平面直角坐标系中,以点C(0,3)为圆心,5为半径作圆,交x轴于A,B两点,交y轴正半轴于P点,以点P为顶点的抛物线经过点A、B两点.
如图,在平面直角坐标系中,以点C(0,3)为圆心,5为半径作圆,交x轴于A,B两点,交y轴正半轴于P点,以点P为顶点的抛物线经过点A、B两点.(1)求出A,B两点的坐标;
(2)求此抛物线的解析式.
考点:垂径定理,待定系数法求二次函数解析式,勾股定理
专题:
分析:(1)连结AC,由题意得CO=3,AC=5,根据勾股定理求出AO的长,再由对称轴的性质即可得出结论;
(2)根据CP=5得出OP=8,故可得出点P的坐标,利用待定系数法可求出抛物线的解析式.
(2)根据CP=5得出OP=8,故可得出点P的坐标,利用待定系数法可求出抛物线的解析式.
解答: 解:(1)连结AC,由题意得CO=3,AC=5.
解:(1)连结AC,由题意得CO=3,AC=5.
∵CO⊥AO,
∴△ACO是直角三角形且∠ACO是直角,
∴AO=
=
=4.
∵由题意可得y轴是抛物线的对称轴,
∴BO=AO=4.
∴点A坐标为(-4,0),点B的坐标为(4,0).
(2)∵CP=5,
∴OP=CO+CP=3+5=8,
∴点P的坐标是( 0,8),
∴可设抛物线解析式为y=ax2+8,
∵抛物线经过点A(-4,0),
∴a(-4)2+8=0
解得a=-
.
∴该抛物线的解析式为y=-
x2+8.
 解:(1)连结AC,由题意得CO=3,AC=5.
解:(1)连结AC,由题意得CO=3,AC=5.∵CO⊥AO,
∴△ACO是直角三角形且∠ACO是直角,
∴AO=
| AC2-CO2 |
| 52-32 |
∵由题意可得y轴是抛物线的对称轴,
∴BO=AO=4.
∴点A坐标为(-4,0),点B的坐标为(4,0).
(2)∵CP=5,
∴OP=CO+CP=3+5=8,
∴点P的坐标是( 0,8),
∴可设抛物线解析式为y=ax2+8,
∵抛物线经过点A(-4,0),
∴a(-4)2+8=0
解得a=-
| 1 |
| 2 |
∴该抛物线的解析式为y=-
| 1 |
| 2 |
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
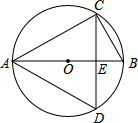 如图,在⊙O中,AB为⊙O的直径,C、D为⊙O上两点,弦AC=
如图,在⊙O中,AB为⊙O的直径,C、D为⊙O上两点,弦AC= 在四边形ABCD中,BD平分∠ABC,AC⊥BD于R,PQ与BC、AD分别相交于点Q、P,且∠BAD=∠BQP.求证:PQ∥CD.
在四边形ABCD中,BD平分∠ABC,AC⊥BD于R,PQ与BC、AD分别相交于点Q、P,且∠BAD=∠BQP.求证:PQ∥CD.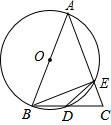 已知,如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°.
已知,如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°.