题目内容
17.(1)填空:21-20=2-1=2( ),22-21=4-2=2( ),23-22=8-4=2( ),…(2)探索(1)中式子的规律,试写出第n个等式,并说明第n个等式成立:
(3)计算:20+21+22+…+299.
分析 (1)根据乘方的运算法则计算即可;
(2)根据式子规律可得2n-2n-1=2n-1,然后利用提公因式2n-1可以证明这个等式成立;
(3)设题中的表达式为a,再根据同底数幂的乘法得出2a的表达式,相减即可.
解答 解:(1)21-20=2-1=20,22-21=4-2=21,23-22=8-4=22;
故答案为:2-1;0;4-2;1;8-4;2;
(2)第n个等式为:2n-2n-1=2n-1,
∵左边=2n-2n-1=2n-1(2-1)=2n-1,
右边=2n-1,
∴左边=右边,∴2n-2n-1=2n-1;
(3)设a=2°+21+22+23+…+298+299.①
则2a=21+22+23+…+298+299+2100②
由②-①得:a=2100-1
∴20+21+22+23+…+298+299=2100-1.
点评 此题主要考查了探寻数列规律问题,认真观察、仔细思考,善用联想是解决这类问题的方法,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出:2n-2n-1=2n-1成立.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
2.已知:12.52=156.25,12.62=158.76,12.72=161.29,12.82=163.84,下列说法正确的是( )
| A. | 12.6<$\sqrt{160}$<12.7 | B. | $\sqrt{160}$=40 | C. | 12.5<$\sqrt{156}$<12.6 | D. | $\sqrt{158.76}$=±12.6 |
 如图△OAB的顶点A的坐标为(3,5),点B(4,0),把△OAB沿x轴向右平移得到△CDE,如果CB=1,那么点D的坐标为(6,5).
如图△OAB的顶点A的坐标为(3,5),点B(4,0),把△OAB沿x轴向右平移得到△CDE,如果CB=1,那么点D的坐标为(6,5). 如图,将周长为16的三角形ABC向右平移2个单位后得到三角形DEF,则四边形ABFD的周长等于20.
如图,将周长为16的三角形ABC向右平移2个单位后得到三角形DEF,则四边形ABFD的周长等于20.
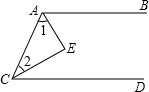 如图,∠BAE=∠DCE=45°,AE⊥CE,通过填空,把下列推理过程补充完整.
如图,∠BAE=∠DCE=45°,AE⊥CE,通过填空,把下列推理过程补充完整.