题目内容
 如图,△ABD≌△ACE,∠AEC=110°,则∠DAE的度数为( )
如图,△ABD≌△ACE,∠AEC=110°,则∠DAE的度数为( )| A、30° | B、40° |
| C、50° | D、60° |
考点:全等三角形的性质
专题:
分析:根据邻补角的定义求出∠AED,再根据全等三角形对应边相等可得AD=AE,然后利用等腰三角形的两底角相等列式计算即可得解.
解答:解:∵∠AEC=110°,
∴∠AED=180°-∠AEC=180°-110°=70°,
∵△ABD≌△ACE,
∴AD=AE,
∴∠AED=∠ADE,
∴∠DAE=180°-2×70°=180°-140°=40°.
故选B.
∴∠AED=180°-∠AEC=180°-110°=70°,
∵△ABD≌△ACE,
∴AD=AE,
∴∠AED=∠ADE,
∴∠DAE=180°-2×70°=180°-140°=40°.
故选B.
点评:本题考查了全等三角形的性质,等腰三角形的判定与性质,熟记性质并准确识图是解题的关键.

练习册系列答案
相关题目
方程3x2-x=2的根的情况是( )
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、没有实数根 |
| D、不确定 |
下列各式中,正确的是( )
A、
| |||
B、(-
| |||
C、±
| |||
D、
|
已知正比例函数y=kx,当x=2时,y=-3,则它的表达式为( )
A、y=-
| ||
B、y=
| ||
C、y=
| ||
D、y=-
|
 如图所示:已知∠ABC=120°,作等边△ACD,将△ACD旋转60°,得到△CDE,AB=3,BC=2,求BD和∠ABD.
如图所示:已知∠ABC=120°,作等边△ACD,将△ACD旋转60°,得到△CDE,AB=3,BC=2,求BD和∠ABD.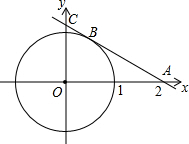 如图,⊙O的半径为1,经过点A(2,0)的直线与⊙O相切于点B,与y轴相交于点C.
如图,⊙O的半径为1,经过点A(2,0)的直线与⊙O相切于点B,与y轴相交于点C.