题目内容
如图，在平行四边形ABCD中，已知∠ODA=90°，AC=26，BD=10，E、F分别是线段OD、OA的中点，则EF的长为考点：平行四边形的性质,三角形中位线定理
专题：
分析：首先利用平行四边形的性质对角线互相平分得出AO．DO的长，再利用勾股定理得出AD的长，进而利用三角形中位线定理与性质得出EF的长．
解答：解：∵在平行四边形ABCD中，∠ODA=90°，AC=26，BD=10，
∴AO=CO=13，BO=DO=5，
故AD=
=
=12，
∵E、F分别是线段OD、OA的中点，
∴EF是△ADO的中位线，
∴EF
AD，
则EF的长为：6．
故答案为：6．
∴AO=CO=13，BO=DO=5，
故AD=
| AO2-DO2 |
| 132-52 |
∵E、F分别是线段OD、OA的中点，
∴EF是△ADO的中位线，
∴EF
| ∥ |
. |
| 1 |
| 2 |
则EF的长为：6．
故答案为：6．
点评：此题主要考查了平行四边形的性质以及勾股定理和三角形中位线定理等知识，得出AD的长是解题关键．
练习册系列答案
名校通行证有效作业系列答案
相关题目
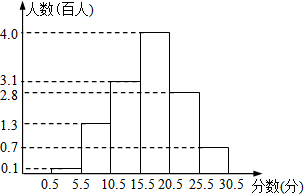2014年3月28日是第19人全国中小学生安全教育日，某校为增强学生的安全意识，组织全校学生参加安全知识测试，并对测试成绩做了详细统计，将测试成绩（成绩都是整数，试卷满分30分）绘制成了如图“频数分布直方图”．请回答：
如图，△ABC是⊙O的内接三角形，如果∠AOC=100°，那么∠B=