题目内容
3.学完一元一次不等式解法后,老师布置了如下练习:解不等式$\frac{15-3x}{2}$≥7-x,并把它的解集在数轴上表示出来.
以下是小明的解答过程:
解:第一步 去分母,得 15-3x≥2(7-x),
第二步 去括号,得 15-3x≥14-2x,
第三步 移项,得-3x+2x≥14-15,
第四步 合并同类项,得-x≥-1,
第五步 系数化为1,得 x≥1.
第六步 把它的解集在数轴上表示为:

老师看后说:“小明的解题过程有错误!”
问:请指出小明从第几步开始出现了错误,并说明判断依据.
答:小明从第三步出现错误,依据是不等式的基本性质1.
分析 根据解一元一次不等式基本步骤:去分母、去括号、移项、合并同类项、系数化为1可得.
解答 解:第一步 去分母,得 15-3x≥2(7-x),
第二步 去括号,得 15-3x≥14-2x,
第三步 移项,得-3x-2x≥14-15,
第四步 合并同类项,得-5x≥-1,
第五步 系数化为1,得x≤$\frac{1}{5}$.
第六步 把它的解集在数轴上表示为:
故答案为:小明从第三步出现错误,依据是不等式的基本性质1.
点评 本题主要考查解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
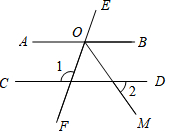 如图,AB∥CD,OM平分∠BOF,∠2=65°,则∠1=130度.
如图,AB∥CD,OM平分∠BOF,∠2=65°,则∠1=130度. 《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开放术、正负术和方程术.其中方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有共买鸡,人出八,盈三;人出七,不足四.问人数、鸡价各几何?”译文:“今天有几个人共同买鸡,每人出8钱,多余3钱,每人出7钱,还缺4钱.问人数和鸡的价钱各是多少?”设人数有x人,鸡的价钱是y钱,可列方程组为$\left\{\begin{array}{l}{8x-3=y}\\{7x+4=y}\end{array}\right.$.
《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开放术、正负术和方程术.其中方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有共买鸡,人出八,盈三;人出七,不足四.问人数、鸡价各几何?”译文:“今天有几个人共同买鸡,每人出8钱,多余3钱,每人出7钱,还缺4钱.问人数和鸡的价钱各是多少?”设人数有x人,鸡的价钱是y钱,可列方程组为$\left\{\begin{array}{l}{8x-3=y}\\{7x+4=y}\end{array}\right.$.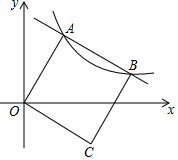 如图,平面直角坐标系中,O为坐标原点,正方形OABC的顶点A,B都在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,边BC与x轴交于点D,则$\frac{BD}{CD}$的值为$\frac{\sqrt{5}-1}{2}$.
如图,平面直角坐标系中,O为坐标原点,正方形OABC的顶点A,B都在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,边BC与x轴交于点D,则$\frac{BD}{CD}$的值为$\frac{\sqrt{5}-1}{2}$.