题目内容
1.已知实数x、y满足x2-$\sqrt{2}$xy-4y2=0,求$\frac{{x}^{2}-\sqrt{2}xy+{y}^{2}}{{x}^{2}+\sqrt{2}xy+{y}^{2}}$的值.分析 首先将原式分解因式,进而得出x,y的关系,进而化简求出答案.
解答 解:∵x2-$\sqrt{2}$xy-4y2=0,
∴(x-2$\sqrt{2}$y)(x+$\sqrt{2}$y)=0,
∴x=2$\sqrt{2}$y,x=-$\sqrt{2}$y,
故当x=2$\sqrt{2}$y时,$\frac{{x}^{2}-\sqrt{2}xy+{y}^{2}}{{x}^{2}+\sqrt{2}xy+{y}^{2}}$=$\frac{4{y}^{2}+{y}^{2}}{(2\sqrt{2}y)^{2}+\sqrt{2}•2\sqrt{2}{y}^{2}+{y}^{2}}$=$\frac{5}{13}$,
当x=-$\sqrt{2}$y时,$\frac{{x}^{2}-\sqrt{2}xy+{y}^{2}}{{x}^{2}+\sqrt{2}xy+{y}^{2}}$=$\frac{5{y}^{2}}{(-\sqrt{2}y)^{2}+\sqrt{2}×(-\sqrt{2}y)•{y}^{2}+{y}^{2}}$=5.
点评 此题主要考查了二次根式的化简求值,正确得出x,y的关系是解题关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 D. ±
D. ±
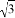 ,y=2+
,y=2+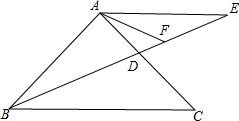 如图,已知等腰△ABC中,AB=AC,点D是AC上一动点,点E在BD的延长线上,且AB=AE,AF平分∠CAE,交DE于F,∠ABC=45°,且BD平分∠ABC,请你证明,BD=2FE.
如图,已知等腰△ABC中,AB=AC,点D是AC上一动点,点E在BD的延长线上,且AB=AE,AF平分∠CAE,交DE于F,∠ABC=45°,且BD平分∠ABC,请你证明,BD=2FE.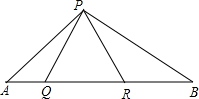 如图,△PQR为等边三角形,∠APB=120°,若AQ=4,QR=6,则BR=9.
如图,△PQR为等边三角形,∠APB=120°,若AQ=4,QR=6,则BR=9. 如图所示,AB∥DC,DC=CB,CE⊥AD,交AD的延长线于E,CF⊥AB垂足为F,∠DAB=∠B,求证:AC平分∠DAB.
如图所示,AB∥DC,DC=CB,CE⊥AD,交AD的延长线于E,CF⊥AB垂足为F,∠DAB=∠B,求证:AC平分∠DAB.
 如图,⊙O的半径为1,点A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.
如图,⊙O的半径为1,点A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.