题目内容
等边△ABC中，AB=9，D在BC上且BD=| 1 |
| 3 |
| 7 |
| 9 |
（1）△ABD与△DCE相似吗？说说你的理由．
（2）求∠ADE的度数．
分析：（1）由等边△ABC中，BD=
BC，AE=
AC，易证得
=
，即可证得△ABD∽△DCE；
（2）由∠ADC=∠BAD+∠B=∠CDE+∠ADE，易求得∠ADE=∠B=60°．
| 1 |
| 3 |
| 7 |
| 9 |
| BD |
| CE |
| AB |
| CD |
（2）由∠ADC=∠BAD+∠B=∠CDE+∠ADE，易求得∠ADE=∠B=60°．
解答：解：（1）△ABD与△DCE相似．
理由：∵△ABC是等边三角形，
∴∠B=∠C=60°，BC=AC=AB，
∵BD=
BC，AE=
AC，
∴CD=
BC，CE=
AC，BD=
AB，
∴CE=
CD，
∴
=
，
即
=
，
∴△ABD∽△DCE；
（2）∵△ABD∽△DCE，
∴∠BAD=∠CDE，
∵∠ADC=∠BAD+∠B=∠CDE+∠ADE，
∴∠ADE=∠B=60°．
理由：∵△ABC是等边三角形，
∴∠B=∠C=60°，BC=AC=AB，
∵BD=
| 1 |
| 3 |
| 7 |
| 9 |
∴CD=
| 2 |
| 3 |
| 2 |
| 9 |
| 1 |
| 3 |
∴CE=
| 1 |
| 3 |
∴
| BD |
| AB |
| CE |
| CD |
即
| BD |
| CE |
| AB |
| CD |
∴△ABD∽△DCE；
（2）∵△ABD∽△DCE，
∴∠BAD=∠CDE，
∵∠ADC=∠BAD+∠B=∠CDE+∠ADE，
∴∠ADE=∠B=60°．
点评：此题考查了相似三角形的判定与性质．此题难度适中，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
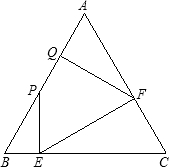如图，在等边△ABC中，AB=4，点P是AB上任意一点，过P作PE⊥BC于E；过E作EF⊥AC于F；过F作FQ⊥AB于Q．设BP=x，AQ=y，用含x的式子填空，并解答有关问题．
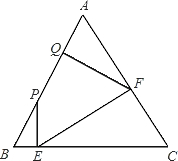如图，在等边△ABC中，AB=2，点P是AB边上任意一点（点P可以与点A重合），过点P作PE⊥BC，垂足为E，过点E作EF⊥AC，垂足为F，过点F作FQ⊥AB，垂足为Q，求当BP的长等于多少时，点P与点Q重合？
作圆，圆心为O，AC、BC分别与⊙O交于点D、E；②延长AB到点P，使BP=OB，连接PE．
（2013•聊城）如图，在等边△ABC中，AB=6，D是BC的中点，将△ABD绕点A旋转后得到△ACE，那么线段DE的长度为
（2013•内江）如图，在等边△ABC中，AB=3，D、E分别是AB、AC上的点，且DE∥BC，将△ADE沿DE翻折，与梯形BCED重叠的部分记作图形L．