题目内容
 (2013•内江)如图,在等边△ABC中,AB=3,D、E分别是AB、AC上的点,且DE∥BC,将△ADE沿DE翻折,与梯形BCED重叠的部分记作图形L.
(2013•内江)如图,在等边△ABC中,AB=3,D、E分别是AB、AC上的点,且DE∥BC,将△ADE沿DE翻折,与梯形BCED重叠的部分记作图形L.(1)求△ABC的面积;
(2)设AD=x,图形L的面积为y,求y关于x的函数解析式;
(3)已知图形L的顶点均在⊙O上,当图形L的面积最大时,求⊙O的面积.
分析:(1)作AH⊥BC于H,根据勾股定理就可以求出AH,由三角形的面积公式就可以求出其值;
(2)如图1,当0<x≤1.5时,由三角形的面积公式就可以表示出y与x之间的函数关系式,如图2,当1.5<x<3时,重叠部分的面积为梯形DMNE的面积,由梯形的面积公式就可以求出其关系式;
(3)如图4,根据(2)的结论可以求出y的最大值从而求出x的值,作FO⊥DE于O,连接MO,ME,求得∠DME=90°,就可以求出⊙O的直径,由圆的面积公式就可以求出其值.
(2)如图1,当0<x≤1.5时,由三角形的面积公式就可以表示出y与x之间的函数关系式,如图2,当1.5<x<3时,重叠部分的面积为梯形DMNE的面积,由梯形的面积公式就可以求出其关系式;
(3)如图4,根据(2)的结论可以求出y的最大值从而求出x的值,作FO⊥DE于O,连接MO,ME,求得∠DME=90°,就可以求出⊙O的直径,由圆的面积公式就可以求出其值.
解答:解:(1)如图3,作AH⊥BC于H,
∴∠AHB=90°.
∵△ABC是等边三角形,
∴AB=BC=AC=3.
∵∠AHB=90°,
∴BH=
BC=
在Rt△ABC中,由勾股定理,得
AH=
.
∴S△ABC=
=
;
(2)如图1,当0<x≤1.5时,y=S△ADE.
作AG⊥DE于G,
∴∠AGD=90°,∠DAG=30°,
∴DG=
x,AG=
x,
∴y=
=
x2,
∵a=
>0,开口向上,在对称轴的右侧y随x的增大而增大,
∴x=1.5时,y最大=
,
如图2,当1.5<x<3时,作MG⊥DE于G,
∵AD=x,
∴BD=DM=3-x,
∴DG=
(3-x),MF=MN=2x-3,
∴MG=
(3-x),
∴y=
,
=-
x2+3
x-
;
(3)如图4,∵y=-
x2+3
x-
;
∴y=-
(x2-4x)-
,
y=-
(x-2)2+
,
∵a=-
<0,开口向下,
∴x=2时,y最大=
,
∵
>
,
∴y最大时,x=2,
∴DE=2,BD=DM=1.作FO⊥DE于O,连接MO,ME.
∴DO=OE=1,
∴DM=DO.
∵∠MDO=60°,
∴△MDO是等边三角形,
∴∠DMO=∠DOM=60°,MO=DO=1.
∴MO=OE,∠MOE=120°,
∴∠OME=30°,
∴∠DME=90°,
∴DE是直径,
S⊙O=π×12=π.
∴∠AHB=90°.
∵△ABC是等边三角形,

∴AB=BC=AC=3.
∵∠AHB=90°,
∴BH=
| 1 |
| 2 |
| 3 |
| 2 |
在Rt△ABC中,由勾股定理,得
AH=
| 3 |
| 2 |
| 3 |
∴S△ABC=
3×
| ||||
| 2 |
| 9 |
| 4 |
| 3 |
(2)如图1,当0<x≤1.5时,y=S△ADE.
作AG⊥DE于G,

∴∠AGD=90°,∠DAG=30°,
∴DG=
| 1 |
| 2 |
| ||
| 2 |
∴y=
x×
| ||||
| 2 |
| ||
| 4 |
∵a=
| ||
| 4 |
∴x=1.5时,y最大=
9
| ||
| 16 |
如图2,当1.5<x<3时,作MG⊥DE于G,
∵AD=x,
∴BD=DM=3-x,
∴DG=
| 1 |
| 2 |

∴MG=
| ||
| 2 |
∴y=
(2x-3+x)
| ||||
| 2 |
=-
| 3 |
| 4 |
| 3 |
| 3 |
| 9 |
| 4 |
| 3 |
(3)如图4,∵y=-
| 3 |
| 4 |
| 3 |
| 3 |
| 9 |
| 4 |
| 3 |
∴y=-
| 3 |
| 4 |
| 3 |
| 9 |
| 4 |
| 3 |
y=-
| 3 |
| 4 |
| 3 |
| 3 |
| 4 |
| 3 |
∵a=-
| 3 |
| 4 |
| 3 |
∴x=2时,y最大=
| 3 |
| 4 |
| 3 |

∵
| 3 |
| 4 |
| 3 |
9
| ||
| 16 |
∴y最大时,x=2,
∴DE=2,BD=DM=1.作FO⊥DE于O,连接MO,ME.
∴DO=OE=1,
∴DM=DO.
∵∠MDO=60°,
∴△MDO是等边三角形,
∴∠DMO=∠DOM=60°,MO=DO=1.
∴MO=OE,∠MOE=120°,
∴∠OME=30°,
∴∠DME=90°,
∴DE是直径,
S⊙O=π×12=π.
点评:本题考查了等边三角形的面积公式的运用,梯形的面积公式的运用,勾股定理的运用,圆周角定理的运用,圆的面积公式的运用,等边三角形的性质的运用,二次函数的性质的运用,解答时灵活运用等边三角形的性质是关键.

练习册系列答案
相关题目
 (2013•内江)如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1:
(2013•内江)如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为3米,台阶AC的坡度为1: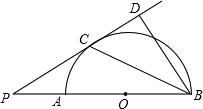 (2013•内江)如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC.
(2013•内江)如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC. (2013•内江)如图,反比例函数
(2013•内江)如图,反比例函数 (2013•内江)如图,正六边形硬纸片ABCDEF在桌面上由图1的起始位置沿直线l不滑行地翻滚一周后到图2位置,若正六边形的边长为2cm,则正六边形的中心O运动的路程为
(2013•内江)如图,正六边形硬纸片ABCDEF在桌面上由图1的起始位置沿直线l不滑行地翻滚一周后到图2位置,若正六边形的边长为2cm,则正六边形的中心O运动的路程为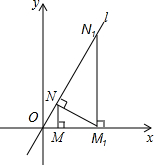 (2013•内江)如图,已知直线l:y=
(2013•内江)如图,已知直线l:y=