题目内容
1．有理数a、b、c在数轴上的位置如图所示，化简$\sqrt{（a-b）^{2}}$-|a+c|+$\sqrt{（c-b）^{2}}$-|-b|．
分析 根据数轴得出a-b＜0，a+c＜0，c-b＜0，-b＜0，进而化简得出即可．
解答 解：由数轴可得：a-b＜0，a+c＜0，c-b＜0，-b＜0，
则$\sqrt{（a-b）^{2}}$-|a+c|+$\sqrt{（c-b）^{2}}$-|-b|
=-（a-b）+（a+c）-（c-b）-b
=-b．
点评 此题主要考查了二次根式以及绝对值的性质与化简，正确化简二次根式是解题关键．
练习册系列答案
相关题目
11．
一个立方体玩具的展开图如图所示．任意掷这个玩具，上表面与底面之和为偶数的概率为（ ）
一个立方体玩具的展开图如图所示．任意掷这个玩具，上表面与底面之和为偶数的概率为（ ）| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
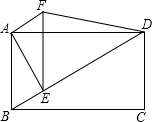如图，四边形ABCD是矩形，E是对角线BD上不同于B，D的任意一点，AF=BE，∠DAF=∠CBD．
如图，在四边形ABCD中，AB∥CD，AB=4，CD=10，点E，F分别为AC，BD的中点，求EF的长．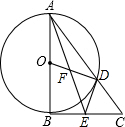
如图，在△ABC中，∠ABC=90°，以AB为直径作⊙O交AC于点D，E是BC的中点，连接AE、OD、DE，AE与OD交于点F．
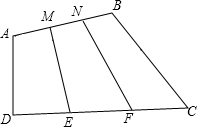如图，四边形ABCD的面积为1，E，F，M，N分别为CD，AB的三等分点，求四边形EFNM的面积．
已知在△ABC中，AB=4，AC=3，AB与AC的夹角为α，设△ABC的面积为S．