题目内容
11．甲乙两人准备在一段长为1200m的笔直公路上进行跑步，甲乙跑步的速度分别是5m/s和6m/s，起跑前乙在起点，甲在乙前面100m处．若同时起跑，则两人从起跑至其中一人先到达终点的过程中，甲乙两人之间的距离y（m）与时间t（s）的函数图象是（ ）| A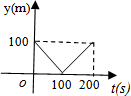． |  | B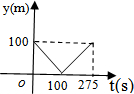． |  | C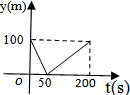． |  | D． |  |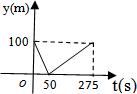
分析 由题意可知，甲在乙前面，而乙的速度大于甲，则此过程为乙先追上甲后再超过甲，全程时间以乙跑的时间计算，算出相遇时间判断图象．
解答 解：此过程可看作追及过程，由相遇到越来越远，按照等量关系“甲在相遇前跑的路程+100=乙在相遇前跑的路程”列出等式
v乙t=v甲t+100，根据
甲、乙跑步的速度分别为5/s和6m/s，起跑前乙在起点，甲在乙前面100米处，
则乙要追上甲，所需时间为t=100s，
乙跑完全程后计时结束，t=1200÷6=200s，
故选：A．
点评 本题考查的是函数图象与实际结合的问题，计算出乙到终点所需的时间是解题的关键，需注意相遇的时间、全程时间以及最后甲乙的距离这几个点．
练习册系列答案
相关题目
3．已知⊙O1和⊙O2的半径分别是3cm和5cm，圆心距O1O2是4cm，则这两个圆的位置关系是（ ）
| A． | 外离 | B． | 相交 | C． | 相切 | D． | 内含 |
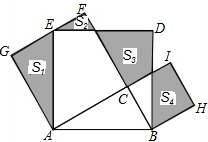如图，Rt△ABC中，∠C=90°，AC=12，BC=5．分别以AB、AC、BC为边在AB的同侧作正方形ABDE、ACFG、BCIH，四块阴影部分的面积分别为S1、S2、S3、S4． 则S1+S2+S3+S4等于（ ）
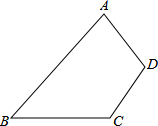四边形ABCD中，∠B=45°，∠C=∠D=120°，AD=CD=12，则AB=12$\sqrt{6}$．