题目内容
 如图,在矩形纸片ABCD中,AB=5CM,BC=10CM,CD上有一点E,ED=2CM,AD上有一点P,PD=3CM,过点P作PF⊥AD,交BC于点F,将纸片折叠,使点P与点E重合,折痕与PF交于点Q,则PQ的长是( )
如图,在矩形纸片ABCD中,AB=5CM,BC=10CM,CD上有一点E,ED=2CM,AD上有一点P,PD=3CM,过点P作PF⊥AD,交BC于点F,将纸片折叠,使点P与点E重合,折痕与PF交于点Q,则PQ的长是( )A、
| ||
| B、3cm | ||
| C、2cm | ||
D、
|
考点:翻折变换(折叠问题)
专题:
分析:如图,首先求出PE=
,进而得到PN=
;证明△PMN∽△PED,求出PM的长度;证明
△MPQ∽△EDP,求出PQ的长度,即可解决问题.
| 13 |
| ||
| 2 |
△MPQ∽△EDP,求出PQ的长度,即可解决问题.
解答: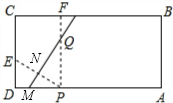 解:如图,由题意得:
解:如图,由题意得:
MN⊥PE,且平分PE;
∵四边形ABCD为矩形,
∴∠D=90°;而ED=2,PD=3,
∴由勾股定理得:PE=
,
∴PN=
;
∵∠EDP=∠MNP,∠DPE=∠NPM,
∴△PMN∽△PED,
∴
=
=
,
∴PM=
同理可证:△MPQ∽△EDP,
∴
=
,
∴PQ=
cm.
故答案为A.
 解:如图,由题意得:
解:如图,由题意得:MN⊥PE,且平分PE;
∵四边形ABCD为矩形,
∴∠D=90°;而ED=2,PD=3,
∴由勾股定理得:PE=
| 13 |
∴PN=
| ||
| 2 |
∵∠EDP=∠MNP,∠DPE=∠NPM,
∴△PMN∽△PED,
∴
| PN |
| PD |
| MN |
| DE |
| PM |
| PE |
∴PM=
| 13 |
| 6 |
同理可证:△MPQ∽△EDP,
∴
| PQ |
| PD |
| PM |
| DE |
∴PQ=
| 13 |
| 4 |
故答案为A.
点评:该题以矩形为载体,以翻折变换为方法,以考查相似三角形的判定及其性质的应用为核心构造而成;对综合的分析问题解决问题的能力提出了一定的要求.

练习册系列答案
相关题目
下列各式正确的是( )
A、
| ||||||
| B、|3.14-π|=π-3.14 | ||||||
C、
| ||||||
D、
|
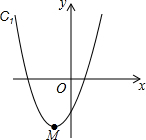 如图所示,已知抛物线C1:y=x2+2x-1的顶点为M,抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移得到抛物线C3,C3的顶点为N,且点M、N关于原点成中心对称,则抛物线C3的解析式为
如图所示,已知抛物线C1:y=x2+2x-1的顶点为M,抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移得到抛物线C3,C3的顶点为N,且点M、N关于原点成中心对称,则抛物线C3的解析式为在Rt△ABC中,∠C=90°,sinA=
.则cosB的值为( )
| 5 |
| 13 |
A、
| ||
B、
| ||
C、
| ||
D、
|
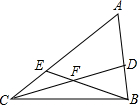 已知:如图,△ABC中,点D、E分别在AB、AC边上,点F是CD中点,连BF交AC于点E,∠ABE+∠CEB=180°,比较线段BD与CE的大小,并证明你的结论.
已知:如图,△ABC中,点D、E分别在AB、AC边上,点F是CD中点,连BF交AC于点E,∠ABE+∠CEB=180°,比较线段BD与CE的大小,并证明你的结论.