题目内容
已知等腰△ABC中,AB=AC,D为AB边上一点,且AD=CD=BC,I为△ACD内切圆的圆心,则∠ABI的度数为 .
考点:三角形的内切圆与内心
专题:
分析:由AB=AC,AD=CD=BC,根据等角对等边的知识,可得∠BAC=∠ACD,∠ABC=∠ACB=∠CDB,设∠BAC=x°,根据等腰三角形的性质得出∠ACD=x°,∠ABC=∠ACB=∠CDB=2x°,然后根据三角形内角和定理得出关于x的方程,解方程即可求得∠BAC的度数,再根据I为△ACD内切圆的圆心,即可求出∠ABI的度数.
解答:解: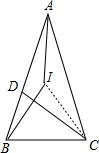 ∵AB=AC,AD=CD=BC,
∵AB=AC,AD=CD=BC,
∴∠BAC=∠ACD,∠B=∠ACB=∠CDB,
设∠BAC=x°,则∠ACD=∠BAC=x°,
∴∠ABC=∠ACB=∠CDB=∠BAC+∠ACD=2x°
∵∠BAC+∠ABC+∠ACB=180°,
∴x+2x+2x=180,
∴x=36,
∴∠BAC=36°,
∴∠ABC∠ACB=72°,
∵I为△ACD内切圆的圆心,
∴∠ABI=36°,
故答案为36°.
 ∵AB=AC,AD=CD=BC,
∵AB=AC,AD=CD=BC,∴∠BAC=∠ACD,∠B=∠ACB=∠CDB,
设∠BAC=x°,则∠ACD=∠BAC=x°,
∴∠ABC=∠ACB=∠CDB=∠BAC+∠ACD=2x°
∵∠BAC+∠ABC+∠ACB=180°,
∴x+2x+2x=180,
∴x=36,
∴∠BAC=36°,
∴∠ABC∠ACB=72°,
∵I为△ACD内切圆的圆心,
∴∠ABI=36°,
故答案为36°.
点评:本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
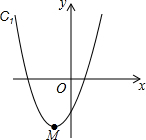 如图所示,已知抛物线C1:y=x2+2x-1的顶点为M,抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移得到抛物线C3,C3的顶点为N,且点M、N关于原点成中心对称,则抛物线C3的解析式为
如图所示,已知抛物线C1:y=x2+2x-1的顶点为M,抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移得到抛物线C3,C3的顶点为N,且点M、N关于原点成中心对称,则抛物线C3的解析式为下列四边形一定有内切圆的是( )
| A、平行四边形 | B、菱形 |
| C、等腰梯形 | D、矩形 |
在Rt△ABC中,∠C=90°,sinA=
.则cosB的值为( )
| 5 |
| 13 |
A、
| ||
B、
| ||
C、
| ||
D、
|
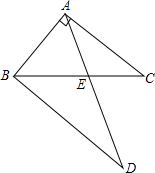 如图,已知△ABC中∠BAC=90°,AB=AC,BD∥AC,∠D=30°,若把△ABD绕点A逆时针旋转一个角度α(0<α<90°),使它与原△ABC的重叠部分为等腰三角形,则α为( )
如图,已知△ABC中∠BAC=90°,AB=AC,BD∥AC,∠D=30°,若把△ABD绕点A逆时针旋转一个角度α(0<α<90°),使它与原△ABC的重叠部分为等腰三角形,则α为( )| A、15°或30° |
| B、30°或45° |
| C、15°或45° |
| D、30°或60° |
 如图是一个正方体纸盒侧面展开图,折成正方体后相对的面上的两个数互为相反数,则A、B、C表示的数为( )
如图是一个正方体纸盒侧面展开图,折成正方体后相对的面上的两个数互为相反数,则A、B、C表示的数为( )A、0,-5,
| ||
B、
| ||
C、
| ||
D、5,
|
 尺规作图:
尺规作图: