题目内容
9.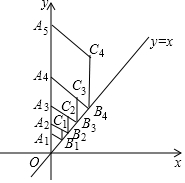 如图,在平面直角坐标系中,点A1的坐标为(0,1),过点A1作直线y=x的垂线,垂足为点B1,以A1B1为边作菱形A1B2C2A3,使得点A2落在y轴上,延长A2C1交直线于点B2,再以A2B2为边作菱形A2B2C2A3,使得点A3落在y轴上…按此作法继续作菱形,则点A2017的坐标是[0,(1+$\frac{\sqrt{2}}{2}$)2016].
如图,在平面直角坐标系中,点A1的坐标为(0,1),过点A1作直线y=x的垂线,垂足为点B1,以A1B1为边作菱形A1B2C2A3,使得点A2落在y轴上,延长A2C1交直线于点B2,再以A2B2为边作菱形A2B2C2A3,使得点A3落在y轴上…按此作法继续作菱形,则点A2017的坐标是[0,(1+$\frac{\sqrt{2}}{2}$)2016].
分析 求出A1~A4的坐标,探究规律后,利用规律解决问题即可.
解答 解:∵点A1的坐标为(0,1),
∴OA1=1,
在Rt△A1B1O中,A1B1=$\frac{\sqrt{2}}{2}$OA1=$\frac{\sqrt{2}}{2}$,
∴A2[0,(1+$\frac{\sqrt{2}}{2}$),
同法可得A2B2=$\frac{\sqrt{2}}{2}$OA2=$\frac{\sqrt{2}}{2}$(1+$\frac{\sqrt{2}}{2}$),
∴OA3=(1+$\frac{\sqrt{2}}{2}$)(1+$\frac{\sqrt{2}}{2}$)=(1+$\frac{\sqrt{2}}{2}$)2,
∴A3[0,(1+$\frac{\sqrt{2}}{2}$)2],
同法可得OA4=(1+$\frac{\sqrt{2}}{2}$)3,
∴A4[0,(1+$\frac{\sqrt{2}}{2}$)3],
…,
A2017[0,(1+$\frac{\sqrt{2}}{2}$)2016].
故答案为[0,(1+$\frac{\sqrt{2}}{2}$)2016].
点评 本题考查菱形的性质、规律型-点的坐标.等腰直角三角形的性质等知识,解题的关键是学会从特殊到一般的探究方法,属于中考常考题型.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
4.下列计算正确的是( )
| A. | 4a2-2a2=2 | B. | (a2)3=a5 | C. | a3•a6=a9 | D. | (2a2)3=6a6 |
5.正整数x、y满足(2x-5)(2y-5)=25,则x+y等于( )
| A. | 18或10 | B. | 18 | C. | 10 | D. | 26 |
19.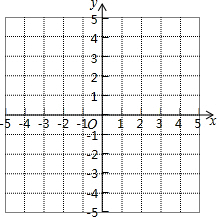 小慧根据学习函数的经验,对函数y=|x-1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:
小慧根据学习函数的经验,对函数y=|x-1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:
(1)函数y=|x-1|的自变量x的取值范围是任意实数;
(2)列表,找出y与x的几组对应值.
其中,b=2;
(3)在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)写出该函数的一条性质:函数的最小值为0(答案不唯一).
 小慧根据学习函数的经验,对函数y=|x-1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:
小慧根据学习函数的经验,对函数y=|x-1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:(1)函数y=|x-1|的自变量x的取值范围是任意实数;
(2)列表,找出y与x的几组对应值.
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | b | 1 | 0 | 1 | 2 | … |
(3)在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)写出该函数的一条性质:函数的最小值为0(答案不唯一).
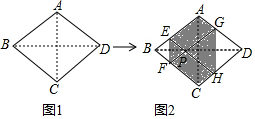 如图1,菱形纸片ABCD的边长为2,∠ABC=60°,翻折∠B,∠D,使点B,D两点重合于对角线BD上一点P,EF,GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断:
如图1,菱形纸片ABCD的边长为2,∠ABC=60°,翻折∠B,∠D,使点B,D两点重合于对角线BD上一点P,EF,GH分别是折痕(如图2).设AE=x(0<x<2),给出下列判断: 在菱形ABCD中,AB=5,AC=8,点P是AC上的一个动点,过点P作EF垂直于AC交AD于点E,交AB于点F,将△AEF沿EF折叠,使点A落在点A'处,当△A'CD
在菱形ABCD中,AB=5,AC=8,点P是AC上的一个动点,过点P作EF垂直于AC交AD于点E,交AB于点F,将△AEF沿EF折叠,使点A落在点A'处,当△A'CD