题目内容
14.如图1,已知MN是⊙O的切线,且点为点C,AB是⊙O的弦,且AB∥MN.(1)求证:AC=BC;
(2)如图2,点D、E分别为$\widehat{AB}$、$\widehat{AC}$上的点,且$\widehat{DB}$=$\widehat{AE}$,连接BE,CD,弦CD分别与BE、AB相交于点G、K.求证:∠EGC=∠A;
(3)如图3,在(2)条件下,连接BD、DA,弦DA的延长线与弦CE的延长线相交于点F,若AF=3$\sqrt{10}$,BC=10$\sqrt{2}$,EC=5$\sqrt{2}$,求线段BK的长.

分析 (1)如图1中,连接CO且延长与AB交于点H,只要证明CH垂直平分线段AB即可解决问题.
(2)利用等量代换,首先证明∠CGE=∠ABC,再由∠ABC=∠BAC即可证明.
(3)如图3中,连接AE,过点A作AQ⊥FC,垂足为Q,过点K作KP⊥FC于P.首先证明AF=AE=3$\sqrt{10}$,FQ=QE,设FQ=m,则有AQ2=(3$\sqrt{10}$)2-m2=(10$\sqrt{2}$)2-(m+5$\sqrt{2}$)2,求出AQ在Rt△AQF中,tan∠F=$\frac{AQ}{FQ}$=$\frac{6\sqrt{2}}{3\sqrt{2}}$=2=tan∠ABC,在Rt△ACQ中,tan∠ACQ=$\frac{AQ}{CQ}$=$\frac{6\sqrt{2}}{8\sqrt{2}}$=$\frac{3}{4}$=tan∠BCD,在Rt△BPK中,tan∠KBP=$\frac{KP}{BP}$=2,设KP=6n,BP=3n,在Rt△CPK中,tan∠KCP=$\frac{KP}{CP}$=$\frac{3}{4}$,可得CP=8n,由BP+CP=BC,可得3n+8n=10$\sqrt{2}$,求出n即可解决问题.
解答 (1)证明:如图1中,连接CO且延长与AB交于点H,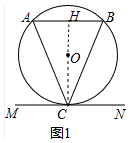
∵MN是⊙O的切线,OC为半径,
∴OC⊥MN,
∴∠OCM=90°,
∵AB∥MN,
∴∠BHC=∠OCM=90°,
∴OH⊥AB,
∵AB是弦,
∴AH=BH,
∴AC=BC.
(2)证明:如图2中,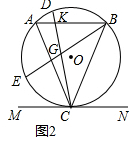
∵$\widehat{AE}$=$\widehat{DB}$,
∴∠ABE=∠DCB,
∵∠EGC=∠DCB+∠EBC,∠ABC=∠ABE+∠EBC,
∴∠EGC=∠ABC,
∵AC=BC,
∴∠A=∠ABC,
∴∠EGC=∠A.
(3)解:如图3中,连接AE,过点A作AQ⊥FC,垂足为Q,过点K作KP⊥FC于P.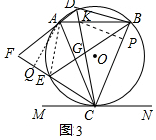
∵BC=10$\sqrt{2}$,
∴AC=BC=10$\sqrt{2}$,
∵$\widehat{AE}$=$\widehat{DB}$,
∴∠ACF=∠DCB,
∴∠FCD=∠ACB,
∵∠ADC=∠ABC,
∴∠F=180°-∠ADC-∠FCD=180°-∠ABC-∠ACB=∠BAC=∠ABC,
∵∠AEF=∠ABC,
∴∠AFE=∠AEF,
∴AF=AE=3$\sqrt{10}$,
∴FQ=QE,设FQ=m,则有AQ2=(3$\sqrt{10}$)2-m2=(10$\sqrt{2}$)2-(m+5$\sqrt{2}$)2,
解得m=3$\sqrt{2}$,
∴AQ=$\sqrt{(3\sqrt{10})^{2}-(3\sqrt{2})^{2}}$=6$\sqrt{2}$,
在Rt△AQF中,tan∠F=$\frac{AQ}{FQ}$=$\frac{6\sqrt{2}}{3\sqrt{2}}$=2=tan∠ABC,
在Rt△ACQ中,tan∠ACQ=$\frac{AQ}{CQ}$=$\frac{6\sqrt{2}}{8\sqrt{2}}$=$\frac{3}{4}$=tan∠BCD,
在Rt△BPK中,tan∠KBP=$\frac{KP}{BP}$=2,设KP=6n,BP=3n,
在Rt△CPK中,tan∠KCP=$\frac{KP}{CP}$=$\frac{3}{4}$,
∴CP=8n,
∵BP+CP=BC,
∴3n+8n=10$\sqrt{2}$,
∴n=$\frac{10\sqrt{2}}{11}$.
∴KB=$\sqrt{(3n)^{2}+(6n)^{2}}$=3$\sqrt{5}$n=$\frac{30\sqrt{10}}{11}$.
点评 本题考查圆综合题、等腰三角形的判定和性质、勾股定理、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数构建方程解决问题,属于中考压轴题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DE保持水平,并且边DE与点B在同一条直线上.已知纸板的两条边DE=70cm,EF=30cm,测得AC=$\frac{7}{8}$m,BD=9m,求树高AB.
如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DE保持水平,并且边DE与点B在同一条直线上.已知纸板的两条边DE=70cm,EF=30cm,测得AC=$\frac{7}{8}$m,BD=9m,求树高AB. 如图,△ABC各顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1).
如图,△ABC各顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1). 如图:甲转盘被分成3个面积相等的扇形、乙转盘被分成2个面积相等的扇形.两圆心中心各有一个可以自由转动的指针,随机地转动指针(当指针指在边界线上时视为无效,重转).请回答下列问题.
如图:甲转盘被分成3个面积相等的扇形、乙转盘被分成2个面积相等的扇形.两圆心中心各有一个可以自由转动的指针,随机地转动指针(当指针指在边界线上时视为无效,重转).请回答下列问题.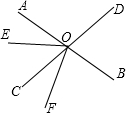 如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.