题目内容
 如图,圆锥的侧面积恰好等于其底面积的2倍,则该圆锥侧面展开图所对应扇形圆心角的度数为( )
如图,圆锥的侧面积恰好等于其底面积的2倍,则该圆锥侧面展开图所对应扇形圆心角的度数为( )| A、180° | B、90° |
| C、120° | D、60° |
考点:圆锥的计算
专题:
分析:设出母线长与底面半径,根据题意和圆的面积,扇形的面积公式求解.
解答:解:设母线长为R,圆锥侧面展开图所对应扇形圆心角的度数为n,底面半径为r.
∴底面周长=2πr,底面面积=πr2,侧面积=
×2πr×R=πRr=2×πr2,
∴R=2r,
∴
=2πr=πR,
∴n=180°
故选A.
∴底面周长=2πr,底面面积=πr2,侧面积=
| 1 |
| 2 |
∴R=2r,
∴
| nπR |
| 180 |
∴n=180°
故选A.
点评:本题利用了扇形的面积公式,圆的面积公式,弧长公式,圆的周长公式求解.注意圆锥的侧面积=底面周长×母线长÷2.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
方程x(x-1)=2(x-1)的根为( )
| A、1 | B、2 | C、1和2 | D、-1和2 |
自然数3的相反数是( )
| A、-3 | ||
| B、3 | ||
C、-
| ||
D、
|
 双曲线y1、y2在第一象限的象如图,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C,若S△AOB=1,则y2的解析式是
双曲线y1、y2在第一象限的象如图,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C,若S△AOB=1,则y2的解析式是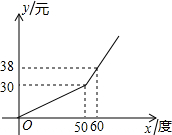 电力公司为增强人们节约用电意识,采取用户每月电量分段计费的方法收费,每月的电费y(元)与用电量x(度)之间的函数关系如图所示.若某用户二、三月的电费分别为39.6元和24元,则该用户三月份比二月份节约用电
电力公司为增强人们节约用电意识,采取用户每月电量分段计费的方法收费,每月的电费y(元)与用电量x(度)之间的函数关系如图所示.若某用户二、三月的电费分别为39.6元和24元,则该用户三月份比二月份节约用电