题目内容
6.一条弦把圆分为长度比为 3:2 的两段弧,那么这条弦所对的圆周角度数为72°或108°.分析 先求出这条弦所对圆心角的度数,然后分情况讨论这条弦所对圆周角的度数.
解答  解:如图,连接OA、OB.
解:如图,连接OA、OB.
弦AB将⊙O分为3:2两部分,
则∠AOB=$\frac{2}{5}$×360°=144°;
∴∠ACB=$\frac{1}{2}$∠AOB=72°,
∠ADB=180°-∠ACB=108°;
故这条弦所对的圆周角的度数为72°或108°
故答案为72°或108°.
点评 本题考查了圆周角定理以及圆内接四边形的性质;需注意的是在圆中,一条弦(非直径)所对的圆周角应该有两种情况,不要漏解.

练习册系列答案
相关题目
14.二次函数y=-2(x-3)2+1的图象的顶点坐标是( )
| A. | (3,1) | B. | (3,-1) | C. | (-3,1) | D. | (-3,-1) |
1.用配方法解一元二次方程 x2+6x+6=0,则方程可变形为( )
| A. | (x-3)2=3 | B. | (x+3)2=3 | C. | (x-6)2=30 | D. | (x+6)2=30 |
11.数据0,1,1,x,3,4的平均数是2,则这组数据的中位数是( )
| A. | 1 | B. | 2 | C. | 2.5 | D. | 3 |
 在压力不变的情况下,某物体承受的压强p(Pa)与它的受力面积S(m2)的反比例函数,其图象如图所示.
在压力不变的情况下,某物体承受的压强p(Pa)与它的受力面积S(m2)的反比例函数,其图象如图所示.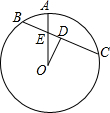 如图,D是⊙O弦BC的中点,A是⊙O上的一点,OA与BC交于点E,已知AO=8,BC=12.
如图,D是⊙O弦BC的中点,A是⊙O上的一点,OA与BC交于点E,已知AO=8,BC=12. 如图,一次函数y=-$\frac{3}{4}$x+3的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90?,求:
如图,一次函数y=-$\frac{3}{4}$x+3的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90?,求: