��Ŀ����
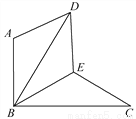
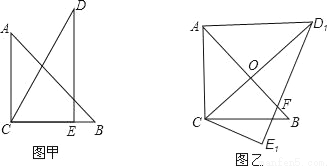
��һ�����ǰ���ͼ���ã����С�ACB=��DEC=90�㣬��A=45�㣬��D=30�㣬б��AB=6��DC=7�������ǰ�DCE�Ƶ�C˳ʱ����ת15��õ���D1CE1����ͼ�ң�����ʱAB��CD1���ڵ�O�����߶�AD1�ij�Ϊ��������
A. 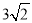 B. 5 C. 4 D.
B. 5 C. 4 D. 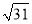
���𰸡�B
������������ת�����ʿ�֪����ͼ���У���BCE1=15�㣬��D1CE1=60�㣬AB=6��CD1=CD=7��
���D1CB=60��-15��=45�㣬
�֡ߡ�ACB=90�㣬
��COƽ�֡�ACB��
�֡�AC=BC��
��CO��AB����CO=AO=BO=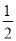 AB=3��
AB=3��
��D1O=CD1-CO=7-3=4����AOD1=90�㣬
����Rt��AOD1��AD1=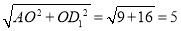 .
.
��ѡB.
�㾦���������Ĺؼ�������ת������֤������D1CB=45�㣬�Ӷ��õ�CD1ƽ�֡�ACB����ϵ��������εġ����ߺ�һ��֤�á�AOD1=90�㣬�����AO=3��OD1=4����������ͱ�úܼ���.
�����͡���ѡ��
��������
10
����ijС��ʵʩ��ů���칤�̣��ּס��������̶ӷֱ�ͬʱ��������600�׳��Ĺܵ������ڹܵ�����y���ף����ھ�ʱ��x���죩֮��Ĺ�ϵ��ͼ��ʾ��������˵���У���ȷ�ĸ����У� ������
�ټ�ÿ����100�ף�
���Ҷӿ��������ÿ����50�ף�
�۵�x=4ʱ���ס����������ڹܵ�������ͬ��
�ܼӱ��Ҷ���ǰ2���������
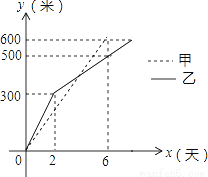
A. 1 B. 2 C. 3 D. 4
D ���������ټ�ÿ����=100��,��ȷ. ���Ҷӿ��������ÿ���ڣ� �ף���ȷ. �۵�x=4ʱ���ס������ӽ�����x=4���������ڹܵ�������ͬ.��ȷ. ���ɢ�֪���������ʱ���һ���100�ף�1002. �ӱ��Ҷ���ǰ2�����������ȷ. ��ѡD.


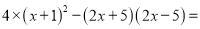 _________.
_________.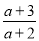 �£�
�£�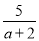 -a+2��������a=2sin60��+3tan45�㣮
-a+2��������a=2sin60��+3tan45�㣮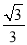 .
.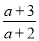 �£�
�£�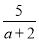 -
-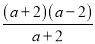 ��
��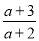 ��
��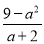 =
=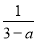 ��
��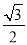 +3��1=
+3��1=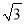 +3
+3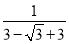 =��
=��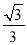 .
.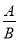 ����ʽ.���B�к�����ĸ,��ô��
����ʽ.���B�к�����ĸ,��ô�� 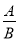 Ϊ��ʽ.��ʽ�ص���û�еȺţ���ʽ�Ӽ�һ����Ҫͨ��.
Ϊ��ʽ.��ʽ�ص���û�еȺţ���ʽ�Ӽ�һ����Ҫͨ��.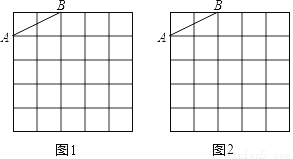
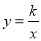 ��k��0����ͼ���ϣ���y1��y2�Ĵ�С��ϵΪ��������
��k��0����ͼ���ϣ���y1��y2�Ĵ�С��ϵΪ��������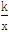 ��ÿ�������ڣ�y��x�����������y1��y2����ѡB.
��ÿ�������ڣ�y��x�����������y1��y2����ѡB.
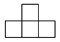 B.
B. 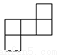 C.
C. 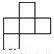 D.
D.