题目内容
10.在直角坐标系中,已知点P在第一象限内,点P与原点O的距离OP=2,点P与原点O的连线与x轴的正半轴的夹角为60°,则点P的坐标是(1,$\sqrt{3}$).分析 作PM⊥x轴于点M,构造直角三角形,根据三角函数的定义求解.
解答 解:作PM⊥x轴于点M,如图所示:
∵OP=2,
∴sin60°=$\frac{PM}{OP}$=$\frac{\sqrt{3}}{2}$,cos60°=$\frac{OM}{OP}$=$\frac{1}{2}$,
∴PM=$\sqrt{3}$,OM=1.
故P点坐标为:(1,$\sqrt{3}$).
故答案为:(1,$\sqrt{3}$).
点评 本题考查了解直角三角形和坐标与图形性质的知识,难度不大,注意掌握一个角的余弦和正弦的计算方法.

练习册系列答案
相关题目
5.已知点P是线段AB的黄金分割点(AP>PB),AB=4,那么AP的长是( )
| A. | $2\sqrt{5}-2$ | B. | $2-\sqrt{5}$ | C. | $2\sqrt{5}-1$ | D. | $\sqrt{5}-2$ |

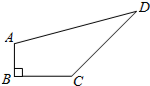 某住宅小区有一块草坪如图所示,已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,这块草坪的面积是36米2.
某住宅小区有一块草坪如图所示,已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,这块草坪的面积是36米2.