Question

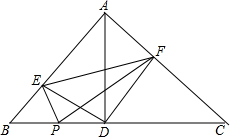已知：如图，在△ABC中，∠BAC=90°，AD⊥BC于点D，点P为BC上任意一点，PE⊥AB于E，PF⊥AC于点F．
（1）求证：△ADF∽△BDE；
（2）求证：△DEF∽△ABC．

Answer 1

考点：相似三角形的判定

专题：证明题

分析：（1）由∠BAC=90°，AD⊥BC，PE⊥AB，PF⊥AC可得到四边形AEPF为矩形，则AF=EP，再利用有两组角对应相等的两个三角形相似得到Rt△BEP∽Rt△BDA，得到

EP

AD

=

BE

BD

，则

AF

AD

=

BE

BD

，利用比例性质变形得

AF

BE

=

AD

BD

，根据等角的余角相等得∠DAF=∠B，根据两组对应边的比相等且夹角对应相等的两个三角形相似可判断△ADF∽△BDE；
（2）由△ADF∽△BDE得到∠ADF=∠BDE，

DF

DE

=

AD

BD

，变形得

DF

AD

=

DE

BD

，再由∠BDF+∠ADE=90°得到∠DEF=90°，于是可证明△DEF∽△DBA，所以∠DEF=∠B，然后根据有两组角对应相等的两个三角形相似得到Rt△DEF∽Rt△ABC．

解答：证明：（1）∵∠BAC=90°，AD⊥BC，PE⊥AB，PF⊥AC，
∴四边形AEPF为矩形，
∴AF=EP，
∵∠EBP=∠DBA，
∴Rt△BEP∽Rt△BDA，
∴

EP

AD

=

BE

BD

，
∴

AF

AD

=

BE

BD

，即

AF

BE

=

AD

BD

，
∵∠DAF+∠BAD=90°，∠B+∠BAD=90°，
∴∠DAF=∠B，
∴△ADF∽△BDE；
（2）∵△ADF∽△BDE，
∴∠ADF=∠BDE，

DF

DE

=

AD

BD

，即

DF

AD

=

DE

BD

而∠BDF+∠ADE=90°，
∴∠ADF+∠ADE=90°，∠DEF=90°，
∴∠ADB=∠FDE，
∴△DEF∽△DBA，
∴∠DEF=∠B，
∴Rt△DEF∽Rt△ABC．

点评：本题考查了相似三角形的判定与性质：两组对应边的比相等且夹角对应相等的两个三角形相似；有两组角对应相等的两个三角形相似．