题目内容
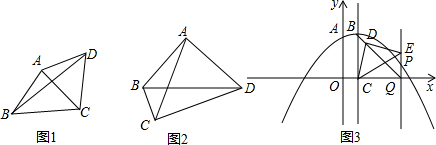
 如图,⊙O1与⊙O2外切于点D,直线l与两圆分别相切于点A、B,与直线
如图,⊙O1与⊙O2外切于点D,直线l与两圆分别相切于点A、B,与直线O1O2相交于点M,且tan∠AM01=
| ||
| 3 |
| 3 |
(1)求⊙O1的半径;
(2)求△ADB内切圆的面积;
(3)在直线l上是否存在点P,使△MO2P相似于△MDB?若存在,求出PO2的长;若不存在,请说明理由.
考点:圆的综合题
专题:综合题
分析:(1)设⊙O1的半径为r.连结O1A,由切线性质可知O1A⊥MA.由题意得∠AM01=30°,因此△MAO1是一个含30度角的直角三角形,所以MO1=2O1A=2r,从而MD=3r=4
,由此求出⊙O1的半径;
(2)利用互余由∠AM02=30°得到∠MO2B=60°,则可判断△O2BD为等边三角形,所以BD=O2B=4
,∠DBO2=60°,于是可计算出∠ABD=30°,同样可得∠MO1A=60°,利用三角形外角性质可计算得∠O1AD=
∠MO1A=30°,则∠DAB=60°,所以∠ADB=90°,在Rt△ABD中,根据含30度的直角三角形三边的关系得AD=
BD=4,AB=2AD=8,利用直角三角形内切圆的半径公式得到△ADB内切圆的半径=
=2
-2,然后根据圆的面积公式求解;
(3)先在Rt△MBO2中,根据含30度的直角三角形三边的关系得MB=
O2B=12,然后分类讨论:△MO2P与△MDB有一个公共角,当△MO2P∽△MDB时,利用相似比可计算出O2P=8
;当△MO2P∽△MBD时,利用相似比可计算出O2P=8.
| 3 |
(2)利用互余由∠AM02=30°得到∠MO2B=60°,则可判断△O2BD为等边三角形,所以BD=O2B=4
| 3 |
| 1 |
| 2 |
| ||
| 3 |
| AD+BD-AB |
| 2 |
| 3 |
(3)先在Rt△MBO2中,根据含30度的直角三角形三边的关系得MB=
| 3 |
| 3 |
解答: 解:(1)设⊙O1的半径为r.
解:(1)设⊙O1的半径为r.
连结O1A,如图,
∵MA为切线,
∴O1A⊥MA.
∵tan∠AM01=
,
∴∠AM01=30°,
∴MO1=2O1A=2r.
∴MD=MO1+O1D=3r=4
,
∴⊙O1的半径r=
.
(2)连结O2B,如图,
∵∠AM02=30°,
∴∠MO2B=60°,
而O2B=O2D,
∴△O2BD为等边三角形,
∴BD=O2B=4
,∠DBO2=60°,
∴∠ABD=30°,
∵∠AM01=30°,
∴∠MO1A=60°,
而O1A=O1D,
∴∠O1AD=∠O1DA,
∴∠O1AD=
∠MO1A=30°,
∴∠DAB=60°,
∴∠ADB=180°-30°-60°=90°,
在Rt△ABD中,AD=
BD=4,AB=2AD=8,
∴△ADB内切圆的半径=
=
=2
-2,
∴△ADB内切圆的面积=π•(2
-2)2=(16-8
)π;
(3)存在.
在Rt△MBO2中,MB=
O2B=
×4
=12,
当△MO2P∽△MDB时,
=
,即
=
,解得O2P=8
;
当△MO2P∽△MBD时,
=
,即
=
,解得O2P=8,
综上所述,满足条件的O2P的长为8或8
.
 解:(1)设⊙O1的半径为r.
解:(1)设⊙O1的半径为r.连结O1A,如图,
∵MA为切线,
∴O1A⊥MA.
∵tan∠AM01=
| ||
| 3 |
∴∠AM01=30°,
∴MO1=2O1A=2r.
∴MD=MO1+O1D=3r=4
| 3 |
∴⊙O1的半径r=
4
| ||
| 3 |
(2)连结O2B,如图,

∵∠AM02=30°,
∴∠MO2B=60°,
而O2B=O2D,
∴△O2BD为等边三角形,
∴BD=O2B=4
| 3 |
∴∠ABD=30°,
∵∠AM01=30°,
∴∠MO1A=60°,
而O1A=O1D,
∴∠O1AD=∠O1DA,
∴∠O1AD=
| 1 |
| 2 |
∴∠DAB=60°,
∴∠ADB=180°-30°-60°=90°,
在Rt△ABD中,AD=
| ||
| 3 |
∴△ADB内切圆的半径=
| AD+BD-AB |
| 2 |
4+4
| ||
| 2 |
| 3 |
∴△ADB内切圆的面积=π•(2
| 3 |
| 3 |
(3)存在.
在Rt△MBO2中,MB=
| 3 |
| 3 |
| 3 |
当△MO2P∽△MDB时,
| O2P |
| DB |
| MO2 |
| MD |
| O2P | ||
4
|
8
| ||
4
|
| 3 |
当△MO2P∽△MBD时,
| O2P |
| BD |
| MO2 |
| MB |
| O2P | ||
4
|
8
| ||
| 12 |
综上所述,满足条件的O2P的长为8或8
| 3 |
点评:本题考查了圆的综合题:熟练掌握切线的性质、两圆相切的性质和直角三角形内切圆的半径;会利用含30度的直角三角形三边的关系和三角形相似比进行几何计算;会运用分类讨论的思想解决数学问题.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
下列方程中,解为x=2的方程是( )
| A、3x-2=3 | ||
| B、4-2(x-1)=1 | ||
| C、6-x=2x | ||
D、
|
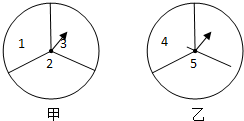 王敏想设计甲、乙两个转盘,通过转转盘来决定张祥与李明谁能得到一张演唱会的门票,每个转盘被分成面积相等的三个扇形区域,并在每个区域内标上不同的数字,数字在1、2、3、4、5、6、7中选,每个数字只能选用一次,转盘甲已经设计好,转盘乙还有一个数字未填.
王敏想设计甲、乙两个转盘,通过转转盘来决定张祥与李明谁能得到一张演唱会的门票,每个转盘被分成面积相等的三个扇形区域,并在每个区域内标上不同的数字,数字在1、2、3、4、5、6、7中选,每个数字只能选用一次,转盘甲已经设计好,转盘乙还有一个数字未填.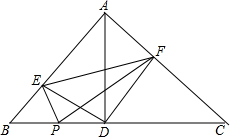 已知:如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,点P为BC上任意一点,PE⊥AB于E,PF⊥AC于点F.
已知:如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,点P为BC上任意一点,PE⊥AB于E,PF⊥AC于点F.