��Ŀ����
��ͼ1����ABC�У�AB=AC����D��BA���ӳ����ϣ���E��BC�ϣ�DE=DC����F��DE��AC�Ľ��㣬��DF=FE��

��1��ͼ1���Ƿ�������BDE��ȵĽǣ������ڣ����ҳ���������֤�����������ڣ�˵�����ɣ�
��2����֤��BE=EC��
��3����������D��BA���ӳ����ϣ���E��BC�ϡ��͡���F��DE��AC�Ľ��㣬��DF=FE���ֱ��Ϊ����D��AB�ϣ���E��CB���ӳ����ϡ��͡���F��ED���ӳ�����AC�Ľ��㣬��DF=kFE���������������䣨��ͼ2������AB=1����ABC=aʱ����BE�ij����ú�k��a��ʽ�ӱ�ʾ����

��1��ͼ1���Ƿ�������BDE��ȵĽǣ������ڣ����ҳ���������֤�����������ڣ�˵�����ɣ�
��2����֤��BE=EC��
��3����������D��BA���ӳ����ϣ���E��BC�ϡ��͡���F��DE��AC�Ľ��㣬��DF=FE���ֱ��Ϊ����D��AB�ϣ���E��CB���ӳ����ϡ��͡���F��ED���ӳ�����AC�Ľ��㣬��DF=kFE���������������䣨��ͼ2������AB=1����ABC=aʱ����BE�ij����ú�k��a��ʽ�ӱ�ʾ����
���㣺�������ۺ���,�����ε��������,ȫ�������ε��ж�������,���������ε�����,ƽ���߷��߶γɱ���,���������ε��ж�������,������Ǻ����Ķ���
ר�⣺�ۺ���
��������1�����õ��������ε����ʼ������ε�������ʾͿɽ�����⣮
��2������E��EG��AC����AB�ڵ�G����ͼ1��Ҫ֤BE=CE��ֻ��֤BG=AG����DF=FE��֤��DA=AG��ֻ��֤��DA=BG��DG=AB��Ҳ��DG=AC���ɣ�ֻ��֤����DCA�ա���EDG���ɽ�����⣮
��3������A��AH��BC������ΪH����ͼ2�������BC=2cos��������E��EG��AC����AB���ӳ����ڵ�G����֤��DCA�ա���EDG������DA=EG��CA=DG=1����֤��ADF�ס�GDE������
=
����DF=kFE�ɵ�DE=EF-DF=��1-k��EF���Ӷ��������AD=
����GE=
����֤��ABC�ס�GBE������
=
���Ӷ��������BE��
��2������E��EG��AC����AB�ڵ�G����ͼ1��Ҫ֤BE=CE��ֻ��֤BG=AG����DF=FE��֤��DA=AG��ֻ��֤��DA=BG��DG=AB��Ҳ��DG=AC���ɣ�ֻ��֤����DCA�ա���EDG���ɽ�����⣮
��3������A��AH��BC������ΪH����ͼ2�������BC=2cos��������E��EG��AC����AB���ӳ����ڵ�G����֤��DCA�ա���EDG������DA=EG��CA=DG=1����֤��ADF�ס�GDE������
| AD |
| DG |
| DF |
| DE |
| k |
| 1-k |
| k |
| 1-k |
| BC |
| BE |
| AC |
| GE |
����⣺��1����DCA=��BDE��
֤������AB=AC��DC=DE��
���ABC=��ACB����DEC=��DCE��
���BDE=��DEC-��DBC=��DCE-��ACB=��DCA��
��2������E��EG��AC����AB�ڵ�G����ͼ1��
����DAC=��DGE��
�ڡ�DCA�͡�EDG�У�
���DCA�ա�EDG��AAS����
��DA=EG��CA=DG��
��DG=AB��
��DA=BG��
��AF��EG��DF=EF��
��DA=AG��
��AG=BG��
��EG��AC��
��BE=EC��
��3������E��EG��AC����AB���ӳ����ڵ�G����ͼ2��
��AB=AC��DC=DE��
���ABC=��ACB����DEC=��DCE��
���BDE=��DBC-��DEC=��ACB-��DCE=��DCA��
��AC��EG��
���DAC=��DGE��
�ڡ�DCA�͡�EDG�У�
���DCA�ա�EDG��AAS����
��DA=EG��CA=DG
��DG=AB=1��
��AF��EG��
���ADF�ס�GDE��
��
=
��
��DF=kFE��
��DE=EF-DF=��1-k��EF��
��
=
��
��AD=
��
��GE=AD=
��
����A��AH��BC������ΪH����ͼ2��
��AB=AC��AH��BC��
��BH=CH��
��BC=2BH��
��AB=1����ABC=����
��BH=AB•cos��ABH=cos����
��BC=2cos����
��AC��EG��
���ABC�ס�GBE��
��
=
��
��
=
��
��BE=
��
��BE�ij�Ϊ
��
֤������AB=AC��DC=DE��
���ABC=��ACB����DEC=��DCE��
���BDE=��DEC-��DBC=��DCE-��ACB=��DCA��
��2������E��EG��AC����AB�ڵ�G����ͼ1��

����DAC=��DGE��
�ڡ�DCA�͡�EDG�У�
|
���DCA�ա�EDG��AAS����
��DA=EG��CA=DG��
��DG=AB��
��DA=BG��
��AF��EG��DF=EF��
��DA=AG��
��AG=BG��
��EG��AC��
��BE=EC��
��3������E��EG��AC����AB���ӳ����ڵ�G����ͼ2��
��AB=AC��DC=DE��
���ABC=��ACB����DEC=��DCE��

���BDE=��DBC-��DEC=��ACB-��DCE=��DCA��
��AC��EG��
���DAC=��DGE��
�ڡ�DCA�͡�EDG�У�
|
���DCA�ա�EDG��AAS����
��DA=EG��CA=DG
��DG=AB=1��
��AF��EG��
���ADF�ס�GDE��
��
| AD |
| DG |
| DF |
| DE |
��DF=kFE��
��DE=EF-DF=��1-k��EF��
��
| AD |
| 1 |
| kEF |
| (1-k)EF |
��AD=
| k |
| 1-k |
��GE=AD=
| k |
| 1-k |
����A��AH��BC������ΪH����ͼ2��
��AB=AC��AH��BC��
��BH=CH��
��BC=2BH��
��AB=1����ABC=����
��BH=AB•cos��ABH=cos����
��BC=2cos����
��AC��EG��
���ABC�ס�GBE��
��
| BC |
| BE |
| AC |
| GE |
��
| 2cos�� |
| BE |
| 1 | ||
|
��BE=
| 2kcos�� |
| 1-k |
��BE�ij�Ϊ
| 2kcos�� |
| 1-k |
���������⿼�������������ε��ж������ʡ�ȫ�������ε��ж������ʡ�ƽ���߷��߶γɱ��������������ε����ʡ������ε�������ʡ�������Ǻ����Ķ����֪ʶ���ۺ��Խ�ǿ����һ�����Ѷȣ�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
������ʽ��
�Ľ⼯Ϊx��1����a��ȡֵ��Χ�ǣ�������
|
| A��a��-1 | B��a��-1 |
| C��a��-1 | D��a��-1 |
 ��ͼ���ڡ�ABC�У�AB=AC=10��BC=12��D��E�ֱ��DZ�BC��AB���е㣬P��BC���ϵĶ��㣨����B��C�غϣ�����BP=x��
��ͼ���ڡ�ABC�У�AB=AC=10��BC=12��D��E�ֱ��DZ�BC��AB���е㣬P��BC���ϵĶ��㣨����B��C�غϣ�����BP=x��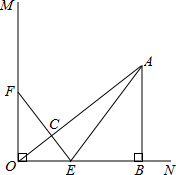 ��ͼ����֪��MON=90�㣬A�ǡ�MON�ڲ���һ�㣬����A��AB��ON������Ϊ��B��AB=3���ף�OB=4���ף�����E��Fͬʱ��O���������E��1.5����/����ٶ���ON�����˶�����F��2����/����ٶ���OM�����˶���EF��OA���ڵ�C������AE������E�����Bʱ����F��ֹ֮ͣ�˶������˶�ʱ��Ϊt�루t��0����
��ͼ����֪��MON=90�㣬A�ǡ�MON�ڲ���һ�㣬����A��AB��ON������Ϊ��B��AB=3���ף�OB=4���ף�����E��Fͬʱ��O���������E��1.5����/����ٶ���ON�����˶�����F��2����/����ٶ���OM�����˶���EF��OA���ڵ�C������AE������E�����Bʱ����F��ֹ֮ͣ�˶������˶�ʱ��Ϊt�루t��0����
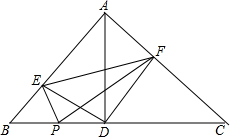 ��֪����ͼ���ڡ�ABC�У���BAC=90�㣬AD��BC�ڵ�D����PΪBC������һ�㣬PE��AB��E��PF��AC�ڵ�F��
��֪����ͼ���ڡ�ABC�У���BAC=90�㣬AD��BC�ڵ�D����PΪBC������һ�㣬PE��AB��E��PF��AC�ڵ�F��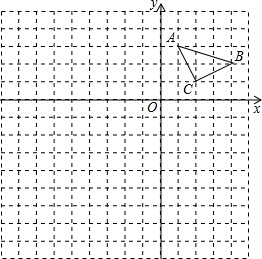 ��ͼ����ABC�Ķ�������ֱ�ΪA��1��3����B��4��2����C��2��1����
��ͼ����ABC�Ķ�������ֱ�ΪA��1��3����B��4��2����C��2��1����