题目内容
11.若x2-13x+1=0,则x2+$\frac{1}{{x}^{2}}$的值为167.分析 把方程两边除以x得到x+$\frac{1}{x}$=13,再利用完全平方公式变形得到x2+$\frac{1}{{x}^{2}}$=(x+$\frac{1}{x}$)2-2,然后利用整体代入的方法计算.
解答 解:∵x2-13x+1=0,
∴x-13+$\frac{1}{x}$=0,即x+$\frac{1}{x}$=13,
∴x2+$\frac{1}{{x}^{2}}$=(x+$\frac{1}{x}$)2-2=169-2=167.
故答案为167.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.

练习册系列答案
相关题目
1. 如图,△ABC中,∠C=90°,AM平分∠CAB,CM=20cm,那么M到AB的距离是( )
如图,△ABC中,∠C=90°,AM平分∠CAB,CM=20cm,那么M到AB的距离是( )
 如图,△ABC中,∠C=90°,AM平分∠CAB,CM=20cm,那么M到AB的距离是( )
如图,△ABC中,∠C=90°,AM平分∠CAB,CM=20cm,那么M到AB的距离是( )| A. | 15cm | B. | 20cm | C. | 25cm | D. | 30cm |
2.一个不透明的盒子有有n个除颜色外其它完全相同的小球,其中有6个黄球,每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后在放回盒子,通过大量重复摸球实验后发现,摸到黄球的频率稳定在20%,那么可以推算出n大约是( )
| A. | 30 | B. | 20 | C. | 12 | D. | 6 |
6.李刚同学的四次数学测试成绩分别是80分、76分、90分、84分,如果按照1:2:4:1的权重对这四次成绩进行综合评价,李刚同学的综合得分应是( )
| A. | 84.5分 | B. | 85分 | C. | 84分 | D. | 83分 |
16.从分别标有数-3,-2,-1,1,2,3的六张没有明显差别的卡片中,随机抽取一张,所抽卡片上的数均大于-2的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
20.已知二次函数y=ax2+bx+c(a≠0)与x轴交于点(x1,0)与(x2,0),其中x1<x2,方程ax2+bx+c-a=0的两根为m、n(m<n),则下列判断正确的是( )
| A. | m<n<x1<x2 | B. | m<x1<x2<n | C. | x1+x2>m+n | D. | b2-4ac≥0 |
1.要制作一个圆锥形的烟囱帽,使底面圆的半径与母线长的比是4:5,那么所需扇形铁皮的圆心角应为( )
| A. | 288° | B. | 144° | C. | 216° | D. | 120° |
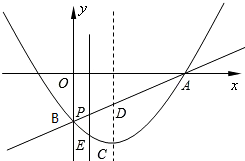 如图,抛物线的顶点为C(1,-2),直线y=kx+m与抛物线交于A、B来两点,其中A点在x轴的正半轴上,且OA=3,B点在y轴上,点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这条抛物线交于点E.
如图,抛物线的顶点为C(1,-2),直线y=kx+m与抛物线交于A、B来两点,其中A点在x轴的正半轴上,且OA=3,B点在y轴上,点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这条抛物线交于点E.