题目内容
 如图,长方形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx-2的图象,过点A和点C,并与y轴交于点E,则k=
如图,长方形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx-2的图象,过点A和点C,并与y轴交于点E,则k=考点:一次函数图象上点的坐标特征
专题:
分析:根据一次函数的解析式即可求得E的坐标,进而求得OE=2,根据三角形相似即可求得OC=4,得出C的坐标,然后代入一次函数的解析式即可求得k的值.
解答:解:∵∠COE=∠ABC=90°,∠ECO=∠ACB,
∴△COE∽△CBA,
∴
=
=2,
∵一次函数y=kx-2,
∴E(0,-2),
∴OE=2,
∴OC=4,
∴C(4,0),
代入y=kx-2得,4k-2=0,
解得k
,
故答案为:
.
∴△COE∽△CBA,
∴
| OC |
| OE |
| BC |
| AB |
∵一次函数y=kx-2,
∴E(0,-2),
∴OE=2,
∴OC=4,
∴C(4,0),
代入y=kx-2得,4k-2=0,
解得k
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查了待定系数法求解析式,三角形相似的判定和性质以及一次函数图象上点的坐标特征.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
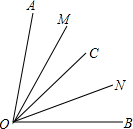 从点O发出的三条射线OA、OB、OC,其中∠AOB=80°,OM、ON分别平分∠AOC,∠BOC.
从点O发出的三条射线OA、OB、OC,其中∠AOB=80°,OM、ON分别平分∠AOC,∠BOC.