题目内容
在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到锐角为30°,则∠B等于 度.
考点:线段垂直平分线的性质,等腰三角形的性质
专题:
分析:此题根据△ABC中∠A为锐角与钝角分为两种情况解答.
解答: 解:(1)当∠A为锐角时,如图,
解:(1)当∠A为锐角时,如图,
∵∠AMN=90°,∠ACM=30°,
∴∠A=90°-30°=60°,
∵AB=AC,
∴∠B=∠ACB=
(180°-∠A)=60°;
 (2)当∠A为钝角时,如图,
(2)当∠A为钝角时,如图,
∵∠AMD=90°,∠ADM=30°,
∴∠DAB=90°-30°=60°,
∵AB=AC,
∴∠B=∠C=
∠DAB=30°.
故答案为60°或30°.
 解:(1)当∠A为锐角时,如图,
解:(1)当∠A为锐角时,如图,∵∠AMN=90°,∠ACM=30°,
∴∠A=90°-30°=60°,
∵AB=AC,
∴∠B=∠ACB=
| 1 |
| 2 |
 (2)当∠A为钝角时,如图,
(2)当∠A为钝角时,如图,∵∠AMD=90°,∠ADM=30°,
∴∠DAB=90°-30°=60°,
∵AB=AC,
∴∠B=∠C=
| 1 |
| 2 |
故答案为60°或30°.
点评:本题考查的是线段垂直平分线的性质以及等腰三角形的性质,此类题需要注意的是要分两种情况解答,考生在考虑问题时要全面.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
等腰三角形两边长分别为5和7,则它的周长是( )
| A、19 | B、11 |
| C、17 | D、17或19 |
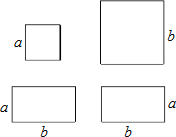 在数学活动课上,李明同学用一个边长为a的正方形和一个边长为b的长方形以及两个长和宽分别为b、a的长方形(如图所示),拼成一个大的正方形,并且他通过比较拼图前后的总面积发现了一个数学规律.
在数学活动课上,李明同学用一个边长为a的正方形和一个边长为b的长方形以及两个长和宽分别为b、a的长方形(如图所示),拼成一个大的正方形,并且他通过比较拼图前后的总面积发现了一个数学规律. 如图中的图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在整个行驶过程中的平均速度为80.8千米/时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.其中正确的说法共有( )
如图中的图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;②汽车在行驶途中停留了0.5小时;③汽车在整个行驶过程中的平均速度为80.8千米/时;④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.其中正确的说法共有( ) 如图,已知四边形ABCD中,AC平分∠BAD,DC=BC,求∠ADC+∠ABC的度数.
如图,已知四边形ABCD中,AC平分∠BAD,DC=BC,求∠ADC+∠ABC的度数. 如图,已知Rt△ABC是⊙O的内接三角形,其中直角边AC=8,BC=6,则⊙O的半径是
如图,已知Rt△ABC是⊙O的内接三角形,其中直角边AC=8,BC=6,则⊙O的半径是