题目内容
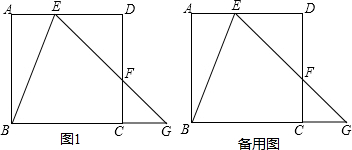
16.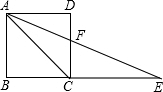 如图,正方形ABCD中,点E在BC的延长线上,AC=CE,则下列结论:
如图,正方形ABCD中,点E在BC的延长线上,AC=CE,则下列结论:(1)∠ACE=135°;(2)∠E=22.5°;(3)∠DFE=112.5°;(4)AF平分∠DAC;(5)DF=FC.
其中正确的有(1)(2)(3)(4).
分析 正方形ABCD中,点E在BC的延长线上,AC=CE,所以∠E=22.5°;∠DFE=112.5°;∠ACE=135°;AF平分∠DAC;均正确,而只有(5)不确定.
解答 解:在正方形ABCD中,
∵AC=CE,
∴∠CAF=∠E,
∵AD∥BC,
∴∠E=∠EAD
∴∠CAF=∠EAD,
∴AE平分∠DAC,
∴∠E=$\frac{1}{2}$×45°=22.5°,
∠DFE=∠E+90°=112.5°
∠ACE=90°+45°=135°,
∵AD∥CE,
∴△AFD∽△EFC,
∴AD:CE=DF:CF,
∵AC=CE=$\sqrt{2}$AD,
∴AD:CE=DF:CF=1:$\sqrt{2}$,
∴DF≠FC.
故(1)(2)(3)(4)正确.
故答案为:(1)(2)(3)(4).
点评 本题考查了正方形的性质,平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质是解题的关键.

练习册系列答案
相关题目
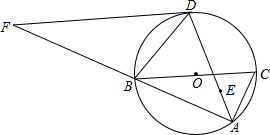 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D,BC是⊙O的直径,⊙O的切线FD与AB的延长线交于点F.
如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D,BC是⊙O的直径,⊙O的切线FD与AB的延长线交于点F. 如图,在△ABC中,∠ABC=100°,∠ACB的平分线交AB边于E,在AC边上有一点D满足∠CBD=20°,连结DE,求∠CED的度数.
如图,在△ABC中,∠ABC=100°,∠ACB的平分线交AB边于E,在AC边上有一点D满足∠CBD=20°,连结DE,求∠CED的度数.