题目内容
1. 如图,已知AB为⊙O的直径,C、D是半圆的三等分点,延长AC,BD交于点E.
如图,已知AB为⊙O的直径,C、D是半圆的三等分点,延长AC,BD交于点E.(1)求∠E的度数;
(2)点M为BE上一点,且满足EM•EB=CE2,连接CM,求证:CM为⊙O的切线.
分析 (1)由半圆的三等分点,得$\widehat{AC}$=$\widehat{CD}$=$\widehat{DB}$,连接OC、OD,则∠AOC=∠COD=∠DOB=60°,证得△AOC、△DOB为正三角形,得出∠EAB=∠EBA=60°,即可得出结果;(2)连接BC,由$\frac{EM}{CE}$=$\frac{CE}{EB}$,∠E=∠E,证得△CEM∽△BEC,由AB为⊙O的直径,得出∠ACB=90°,∠ECB=90°,由△CEM∽△BEC得出∠EMC=∠ECB=90°,由∠AOC=∠DOB=60°,证得OC∥BE,证得∠OCM=90°,即可得出结论.
解答 (1)解: ∵C、D是半圆的三等分点,
∵C、D是半圆的三等分点,
∴$\widehat{AC}$=$\widehat{CD}$=$\widehat{DB}$,
连接OC、OD,如图1所示:
∵AB为⊙O的直径,
∴∠AOC=∠COD=∠DOB=60°,
∵OA=OC=OD=OB,
∴△AOC、△DOB为正三角形,
∴∠EAB=∠EBA=60°,
∴∠E=60°;
(2)证明:连接BC,如图2所示:
∵EM•EB=CE2,
∴$\frac{EM}{CE}$=$\frac{CE}{EB}$,
∵∠E=∠E,
∴△CEM∽△BEC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠ECB=90°,
∴∠EMC=∠ECB=90°,
∵∠AOC=∠DOB=60°,
∴OC∥BE,
∵∠EMC=90°,
∴∠OCM=90°,
∴OC⊥CM,
∴CM为⊙O的切线.
点评 本题考查了相似三角形的判定与性质、切线的判定、圆周角定理、正三角形的判定与性质等知识;熟练掌握正三角形的判定与性质、相似三角形的判定与性质是解决问题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
9.使不等式x-1≥2与3x-7<8同时成立的x的整数值是( )
| A. | 3,4 | B. | 4,5 | C. | 3,4,5 | D. | 4 |
13.对于数据:6,3,4,7,6,0,9,下列判断中正确的是( )
| A. | 这组数据的平均数是6,中位数是6 | B. | 这组数据的平均数是5,中位数是6 | ||
| C. | 这组数据的平均数是6,中位数是7 | D. | 这组数据的平均数是5,中位数是7 |
10.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (a3)2=a9 | C. | (-$\frac{1}{2}$)-2=4 | D. | (sin30°-π)0=0 |
11.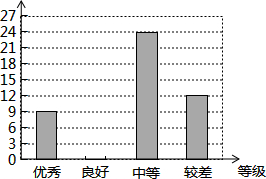 为进一步加强学习贯彻2015年新修订的《中小学生守则》,某校组织全校学生参加安溪县中小学“学守则•促文明•行规范”校园猜谜比赛,将比赛成绩分为“优秀、良好、中等、较差”四个等级.现从中随机抽取该校部分学生的比赛成绩进行统计分析,并制成了如下的统计图表:
为进一步加强学习贯彻2015年新修订的《中小学生守则》,某校组织全校学生参加安溪县中小学“学守则•促文明•行规范”校园猜谜比赛,将比赛成绩分为“优秀、良好、中等、较差”四个等级.现从中随机抽取该校部分学生的比赛成绩进行统计分析,并制成了如下的统计图表:
根据图表信息,回答下列问题:
(1)本次抽查的学生共有60名;
(2)统计表中所表示的数a=15,b=20%,并将条形统计图补充完整;
(3)已知该校共有1800名学生参加比赛,请你估计比赛成绩达到“良好”或“优秀”等级的人数约是多少?
 为进一步加强学习贯彻2015年新修订的《中小学生守则》,某校组织全校学生参加安溪县中小学“学守则•促文明•行规范”校园猜谜比赛,将比赛成绩分为“优秀、良好、中等、较差”四个等级.现从中随机抽取该校部分学生的比赛成绩进行统计分析,并制成了如下的统计图表:
为进一步加强学习贯彻2015年新修订的《中小学生守则》,某校组织全校学生参加安溪县中小学“学守则•促文明•行规范”校园猜谜比赛,将比赛成绩分为“优秀、良好、中等、较差”四个等级.现从中随机抽取该校部分学生的比赛成绩进行统计分析,并制成了如下的统计图表:| 比赛成绩等级 | 人数 | 百分比 |
| 较差 | 12 | b |
| 中等 | 24 | c |
| 良好 | a | 25% |
| 优秀 | 9 | 15% |
(1)本次抽查的学生共有60名;
(2)统计表中所表示的数a=15,b=20%,并将条形统计图补充完整;
(3)已知该校共有1800名学生参加比赛,请你估计比赛成绩达到“良好”或“优秀”等级的人数约是多少?
 如图,在△ABC中,∠ACB=90°,AC=BC,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.
如图,在△ABC中,∠ACB=90°,AC=BC,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G. 如图所示,在正方形铁皮中,剪下一个圆和一个扇形,使余料尽量少.用圆做圆锥的底面,用扇形做圆锥的侧面,正好围成一个圆锥,若圆的半径为2,则扇形的半径为8.
如图所示,在正方形铁皮中,剪下一个圆和一个扇形,使余料尽量少.用圆做圆锥的底面,用扇形做圆锥的侧面,正好围成一个圆锥,若圆的半径为2,则扇形的半径为8.