题目内容
7．已知a、b、c为△ABC的三边长，且a2+b2=8a+12b-52，其中c是△ABC中最短的边长，且c为整数，则c=3．分析 由a2+b2=8a+12b-52，得a，b的值．进一步根据三角形一边边长大于另两边之差，小于它们之和，则b-a＜c＜a+b，即可得到答案．
解答 解：∵a2+b2=8a+12b-52
∴a2-8a+16+b2-12b+36=0
∴（a-4）2+（b-6）2=0
∴a=4，b=6
∴6-4＜c＜6+4
即 2＜c＜10，
且c＜4．
∴整数c可取3．
故答案为：3．
点评 此题考查了因式分解的实际运用，非负数的性质以及三角形的三边关系，分组利用完全平方公式分解因式是解决问题的关键．
练习册系列答案
相关题目
15．下列计算正确的是（ ）
| A． | （2a2）3=8a5 | B． | （$\sqrt{3}$）2=9 | C． | 3$\sqrt{2}$-$\sqrt{2}$=3 | D． | -a8÷a4=-a4 |
12．已知a、b、c是三角形的三边长，如果满足（a-6）2+$\sqrt{b-8}$+|c-10|=0，则三角形的形状是（ ）
| A． | 直角三角形 | B． | 等边三角形 | ||
| C． | 钝角三角形 | D． | 底与腰不相等的等腰三角形 |
19．
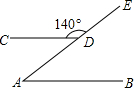如图，点A、D在射线AE上，直线AB∥CD，∠CDE=140°，那么∠A的度数为（ ）
如图，点A、D在射线AE上，直线AB∥CD，∠CDE=140°，那么∠A的度数为（ ）| A． | 140° | B． | 60° | C． | 50° | D． | 40° |
16．下列图形中，既是轴对称图形又是中心对称图形的有（ ）
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |