题目内容
15.一个三角形的三条中位线的长分别为3,4,5,则三角形的面积为24.分析 根据三角形的中位线定理即可求得△ABC的各个边长,利用勾股定理的逆定理可以判断△ABC是直角三角形,则面积即可求解.
解答 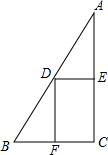 解:设中位线DE=3,DF=4,EF=5.
解:设中位线DE=3,DF=4,EF=5.
∵DE是△ABC的中位线,
∴BC=2DE=2×3=6.
同理:AC=2DF=8,AB=2EF=10.
∵62+82=100=102,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,且∠ACB=90°,
∴S△ABC=$\sqrt{\frac{1}{2}}$AC•BC=$\frac{1}{2}$×6×8=24.
故答案是:24.
点评 本题主要考查了勾股定理,以及三角形的中位线定理,正确求得△ABC的边长,判断△ABC是直角三角形是解题关键.

练习册系列答案
相关题目
6.某新办高新产业2011年的两笔贷款记录如下表:
(1)求两笔贷款的数额各是多少?
(2)已知这两笔贷款的20%用于6月1日前的科研开发,另一部分从6月至11月投入生产新研发出的A、B种新专利产品,新产品的成本与出厂价如上表.到12月1日卖出所有产品,所获利润偿还两笔贷款后,还余200万元.求:两种产品的产量各是多少件?
| 贷款日期 | 月利率% | 还款日期 | 贷款金额(万元) | 还款金额(万元) |
| 4月1日 | 1.5 | 12月1日 | ||
| 6月1日 | 1 | 12月1日 | ||
| 合计 | 300 | 330 |
| A(元) | B(元) | |
| 单件成本 | 3000 | 2000 |
| 单件出厂价 | 6500 | 6000 |
20.到x轴的距离为3的点的坐标可能是( )
| A. | (3,1) | B. | (-3,1) | C. | (1,-3) | D. | (3,2) |
 把一张宽度相等的纸条按如图所示的方式折叠,则∠1=65°.
把一张宽度相等的纸条按如图所示的方式折叠,则∠1=65°. 如图,同学们上体育课时,老师测量学生的跳远成绩,其测量的主要依据是垂线段最短.
如图,同学们上体育课时,老师测量学生的跳远成绩,其测量的主要依据是垂线段最短.