Question

17．如图，一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A（-2，1），B（1，n）两点．
（1）利用图中条件，求n的值并求出反比例函数和一次函数的解析式；
（2）根据图象直接写出kx+b＞$\frac{m}{x}$时x的取值范围；
（3）求△ABO的面积．

Answer 1

分析 （1）把A坐标代入反比例解析式求出m的值，确定出反比例解析式，再将B坐标代入反比例解析式求出n的值，确定出B坐标，将A与B坐标代入一次函数解析式求出k与b的值，即可确定出一次函数解析式；
（2）根据一次函数与反比例函数的交点坐标，结合图形，找出满足题意不等式的解集即可；
（3）对于一次函数，确定出C与D坐标，三角形AOB面积=三角形AOC面积+三角形COD面积+三角形BOD面积，求出即可．

解答 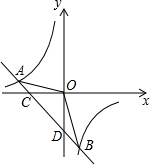解：（1）把A（-2，1）代入反比例解析式得：m=-2，即反比例解析式为y=-$\frac{2}{x}$，
把B（1，n）代入反比例解析式得：n=-2，即B（1，-2），
把A（-2，1）与B（1，-2）代入一次函数解析式得：$\left\{\begin{array}{l}{-2k+b=1}\\{k+b=-2}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=-1}\\{b=-1}\end{array}\right.$，
则一次函数解析式为y=-x-1；
（2）∵一次函数与反比例函数的交点为A（-2，1），B（1，-2），
∴由图象得：kx+b＞$\frac{m}{x}$时x的取值范围为x＜-2或0＜x＜1；
（3）对于一次函数y=-x-1，
令x=0，得到y=-1；令y=0，得到x=-1，即C（-1，0），D（0，-1），
∴OC=OD=1，
则S_△AOB=S_△AOC+S_△COD+S_△BOD=$\frac{1}{2}$×1×1+$\frac{1}{2}$×1×1+$\frac{1}{2}$×1×1=$\frac{3}{2}$．

点评 此题考查了一次函数与反比例函数的交点问题，利用了数形结合的思想，熟练掌握一次函数与反比例函数的性质是解本题的关键．