题目内容
A,∠B为Rt△ABC的两个锐角,且sinA,cosB是方程 的两个实根.求m的值及∠A,∠B的度数.
的两个实根.求m的值及∠A,∠B的度数.
解:∵∠A,∠B为Rt△ABC的两个锐角,∴sinA=cosB,
∵sinA,cosB是方程 的两个实根,
的两个实根,
∴sinA+cosB= ,解得sinA=cosB=
,解得sinA=cosB= ,∴∠A=∠B=45°,
,∴∠A=∠B=45°,
∴sinA•cosB=m,∴m= .
.
分析:根据三角函数的定义知sinA=cosB,由根与系数的关系得,sinA+cosB= ,解得sinA=cosB=
,解得sinA=cosB= ,求出∠A,∠B的度数,由两根之积求得m的值.
,求出∠A,∠B的度数,由两根之积求得m的值.
点评:本题综合考查了三角函数与一元二次方程,解这类题的关键是利用直角三角形,用三角函数来寻求未知系数的等量关系.
∵sinA,cosB是方程
 的两个实根,
的两个实根,∴sinA+cosB=
 ,解得sinA=cosB=
,解得sinA=cosB= ,∴∠A=∠B=45°,
,∴∠A=∠B=45°,∴sinA•cosB=m,∴m=
 .
.分析:根据三角函数的定义知sinA=cosB,由根与系数的关系得,sinA+cosB=
 ,解得sinA=cosB=
,解得sinA=cosB= ,求出∠A,∠B的度数,由两根之积求得m的值.
,求出∠A,∠B的度数,由两根之积求得m的值.点评:本题综合考查了三角函数与一元二次方程,解这类题的关键是利用直角三角形,用三角函数来寻求未知系数的等量关系.

练习册系列答案
相关题目
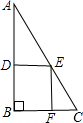 如图,E为Rt△ABC斜边上一点,四边形BFED为正方形,若BC=6,AB=8,则正方形BFED的边长为( )
如图,E为Rt△ABC斜边上一点,四边形BFED为正方形,若BC=6,AB=8,则正方形BFED的边长为( )A、
| ||
B、
| ||
| C、4 | ||
| D、3 |
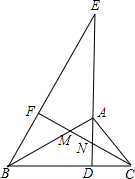 已知,如图,AD为Rt△ABC斜边BC上的高,点E为DA延长线上一点,连接BE,过点C作CF⊥BE于点F,交AB、AD于M、N两点.
已知,如图,AD为Rt△ABC斜边BC上的高,点E为DA延长线上一点,连接BE,过点C作CF⊥BE于点F,交AB、AD于M、N两点.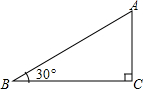 如图,在Rt△ABC中,∠C=90°,∠B=30°.P是AB上的动点(P异于A、B),过点P的直线截Rt△ABC,使截得的三角形与Rt△ABC相似,当
如图,在Rt△ABC中,∠C=90°,∠B=30°.P是AB上的动点(P异于A、B),过点P的直线截Rt△ABC,使截得的三角形与Rt△ABC相似,当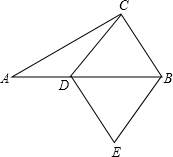 (2013•武汉模拟)如图在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD=
(2013•武汉模拟)如图在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD= 已知:如图,四边形ADCP为平行四边形,M为Rt△ABC斜边AB的中点,连接PM并延长到点E,使PM=ME,连接DE.
已知:如图,四边形ADCP为平行四边形,M为Rt△ABC斜边AB的中点,连接PM并延长到点E,使PM=ME,连接DE.