题目内容
14.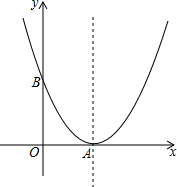 如图,以A为顶点的抛物线与y轴交于点B.已知A、B两点的坐标分别为(3,0)、(0,4).
如图,以A为顶点的抛物线与y轴交于点B.已知A、B两点的坐标分别为(3,0)、(0,4).(1)求抛物线的解析式;
(2)设M是抛物线上的一点,且它位于对称轴的右侧.若四边形OAMB的四条边的长度是四个连续的整数,求点M的坐标;
(3)在(2)的条件下,P是抛物线对称轴上的任意一点,求证:PA2+PB2+PM2>28.
分析 (1)根据待定系数法,可得函数解析式;
(2)根据函数图象上的点满足函数解析式,可得n=$\frac{4}{9}$(m-3)2,根据m、n是正整数,可得m是3的倍数,根据勾股定理,可得MA的长,可得答案;
(3)根据勾股定理,可得MB,MB的长,根据二次函数的性质,可得答案.
解答 (1)解:设y=a(x-3)2,把B(0,4)代入,得a=$\frac{4}{9}$,
∴y=$\frac{4}{9}$(x-3)2;
(2)解:∵m,n为正整数,n=$\frac{4}{9}$(m-3)2,
∴(m-3)2应该是9的整数,
∴m是3的倍数,
又∵m>3,
∴m=6,9,12…,
当m=6时,n=4,此时MA=5,MB=6,
∴四边形OAMB的四边长为3,4,5,6,
当m≥9时,MB>6,
∴四边形OAMB的四边长不能是四个连续的正整数,
∴点M坐标只有一种可能(6,4);
3)证明:设P(3,t),MB与对称轴交点为D,
则PA=|t|,PD=|4-t|,PM2=PB2=(4-t)2+9,
∴PA2+PB2+PM2=t2+2[(4-t)2+9]=3t2-16t+50=3(t-$\frac{8}{3}$)2+$\frac{86}{3}$,
∴当t=$\frac{8}{3}$时,(PA2+PB2+PM2)最小=$\frac{86}{3}$,
∴PA2+PB2+PM2>28总是成立.
点评 本题考查了二次函数综合题,把函数解析式设为顶点式是求函数解析式的关键;利用函数图象上的点满足函数解析式得出m是3的倍数是解题关键;利用了二次函数的性:a>0时,顶点的坐标是函数的最小值.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
4.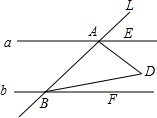 如图,已知直线L交直线a,b于A,B两点,且a∥b,E是a上的点,F是b上的点,满足∠DAE=$\frac{1}{3}$∠BAE,∠DBF=$\frac{1}{3}$∠ABF,则∠ADB的度数是( )
如图,已知直线L交直线a,b于A,B两点,且a∥b,E是a上的点,F是b上的点,满足∠DAE=$\frac{1}{3}$∠BAE,∠DBF=$\frac{1}{3}$∠ABF,则∠ADB的度数是( )
 如图,已知直线L交直线a,b于A,B两点,且a∥b,E是a上的点,F是b上的点,满足∠DAE=$\frac{1}{3}$∠BAE,∠DBF=$\frac{1}{3}$∠ABF,则∠ADB的度数是( )
如图,已知直线L交直线a,b于A,B两点,且a∥b,E是a上的点,F是b上的点,满足∠DAE=$\frac{1}{3}$∠BAE,∠DBF=$\frac{1}{3}$∠ABF,则∠ADB的度数是( )| A. | 45° | B. | 50° | C. | 60° | D. | 无法确定 |
19.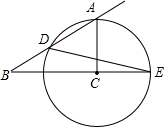 如图,已知△ABC中,∠ACB=90°,∠B=30°,以C为圆心,CA为半径的⊙C交AB于点D,交BC的延长线于点E,则∠E的度数为( )
如图,已知△ABC中,∠ACB=90°,∠B=30°,以C为圆心,CA为半径的⊙C交AB于点D,交BC的延长线于点E,则∠E的度数为( )
 如图,已知△ABC中,∠ACB=90°,∠B=30°,以C为圆心,CA为半径的⊙C交AB于点D,交BC的延长线于点E,则∠E的度数为( )
如图,已知△ABC中,∠ACB=90°,∠B=30°,以C为圆心,CA为半径的⊙C交AB于点D,交BC的延长线于点E,则∠E的度数为( )| A. | 5° | B. | 10° | C. | 15° | D. | 20° |
 已知:如图,AB=AC,AB的垂直平分线MN交AC于点D.若AB=11cm,BC=6cm,求△DBC的周长.
已知:如图,AB=AC,AB的垂直平分线MN交AC于点D.若AB=11cm,BC=6cm,求△DBC的周长. 如图所示,村庄A要从河流L引水入庄,需修筑一水渠,请你画出修筑水渠的最近路线图,标出取水口O.
如图所示,村庄A要从河流L引水入庄,需修筑一水渠,请你画出修筑水渠的最近路线图,标出取水口O.