题目内容
19.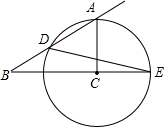 如图,已知△ABC中,∠ACB=90°,∠B=30°,以C为圆心,CA为半径的⊙C交AB于点D,交BC的延长线于点E,则∠E的度数为( )
如图,已知△ABC中,∠ACB=90°,∠B=30°,以C为圆心,CA为半径的⊙C交AB于点D,交BC的延长线于点E,则∠E的度数为( )| A. | 5° | B. | 10° | C. | 15° | D. | 20° |
分析 延长AC交⊙O于点F,连接EF,先根据三角形内角和定理求出∠DAF的度数,再由圆周角定理求出∠CEF的度数,进而可得出结论.
解答  解:延长AC交⊙O于点F,连接EF,
解:延长AC交⊙O于点F,连接EF,
∵△ABC中,∠ACB=90°,∠B=30°,
∴∠BAC=60°,
∴∠DEF=60°.
∵∠ACB=90°,
∴∠BCF=90°,
∴∠CEF=45°,
∴∠BED=∠DEF-∠CEF=60°-45°=15°.
故选C.
点评 本题考查的是圆周角定理,根据题意作出辅助线,构造出圆周角是解答此题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
9. 根据输入的有理数,按图中程序计算,并把输出的结果填入表内:
根据输入的有理数,按图中程序计算,并把输出的结果填入表内:
 根据输入的有理数,按图中程序计算,并把输出的结果填入表内:
根据输入的有理数,按图中程序计算,并把输出的结果填入表内:| 输入 | 输出 |
| 1 | 6 |
| -6 | 4 |
4.下列结论不正确的是( )
| A. | 若a>0,b<0,且a>|b|,则a+b<0 | B. | 若a<0,b>0,且|a|>b,则a+b<0 | ||
| C. | 若a>0,b>0,则a+b>0 | D. | 若a<0,b<0,则a+b<0 |
8.要使分式$\frac{x+3}{(x+3)(x-4)}$有意义,则x应满足( )
| A. | x≠-3 | B. | x≠4 | C. | x≠±3 | D. | x≠-3且x≠4 |
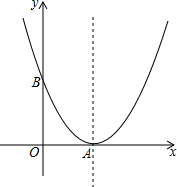 如图,以A为顶点的抛物线与y轴交于点B.已知A、B两点的坐标分别为(3,0)、(0,4).
如图,以A为顶点的抛物线与y轴交于点B.已知A、B两点的坐标分别为(3,0)、(0,4).