题目内容
6.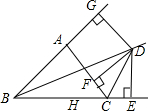 如图,已知BD是∠ABC的内角平分线,CD是∠ACB的外角平分线,由D出发,作点D到BC、AC和AB的垂线DE、DF和DG,垂足分别为E、F、G,则DE、DF、DG的关系是DE=DF=DG.
如图,已知BD是∠ABC的内角平分线,CD是∠ACB的外角平分线,由D出发,作点D到BC、AC和AB的垂线DE、DF和DG,垂足分别为E、F、G,则DE、DF、DG的关系是DE=DF=DG.
分析 由已知条件,根据角平分线上的点到角的两边的距离相等的性质得到线段相等,利用等量代换结论可得.
解答 解:∵BD是∠ABC的内角平分线,DG⊥AB,DE⊥BC,
∴DG=DE,
∵CD是∠ACB的外角平分线,DE⊥BC,DF⊥AC,
∴DE=DF,
∴DE=DF=DG.
故答案为:DE=DF=DG.
点评 本题主要考查角平分线的性质;利用线段的等量代换是正确解答本题的关键.

练习册系列答案
相关题目
16.点P,Q都是直线l外的点,下列说法正确的是( )
| A. | 连接PQ,则PQ一定与直线l垂直 | B. | 连接PQ,则PQ一定与直线l平行 | ||
| C. | 连接PQ,则PQ一定与直线l相交 | D. | 过点P只能画一条直线与直线l平行 |
17.观察下列4个命题:其中真命题是( )
(1)三角形的外角和是180°;
(2)三角形的三个内角中至少有两个锐角;
(3)如果x2y<0,那么y<0;
(4)直线a、b、c,如果a⊥b、b⊥c,那么a⊥c.
(1)三角形的外角和是180°;
(2)三角形的三个内角中至少有两个锐角;
(3)如果x2y<0,那么y<0;
(4)直线a、b、c,如果a⊥b、b⊥c,那么a⊥c.
| A. | (1)(2) | B. | (2)(3) | C. | (2)(4) | D. | (3)(4) |
15.为了激发学生学习英语的兴趣,某中学举行了校园英文歌曲大赛,并设立了一、二、三等奖.学校计划根据设奖情况共买50件奖品,其中购买二等奖奖品件数比一等奖奖品件数的2倍还少10件,购买三等奖奖品所花钱数不超过二等奖所花钱数的1.5倍,且三等奖奖品数不能少于前两种奖品数之和.其中各种奖品的单价如下表所示,如果计划一等奖奖品买x件,买50件奖品的总费用是w元.
(1)用含有x的代数式表示:该校团委购买二等奖奖品多少件,三等奖奖品多少件?并用x的代数式表示w.
(2)请问共有哪几种方案?
(3)请你计算一下,学校应如何购买这三种奖品,才能使所支出的总费用最少,最少是多少元?
| 奖品 | 一等奖奖品 | 二等奖奖品 | 三等奖奖品 |
| 单价(元) | 20 | 10 | 5 |
(2)请问共有哪几种方案?
(3)请你计算一下,学校应如何购买这三种奖品,才能使所支出的总费用最少,最少是多少元?
16.分解因式b2(x-2)+b(2-x)正确的结果是( )
| A. | (x-2)(b2+b) | B. | b(x-2)(b+1) | C. | (x-2)(b2-b) | D. | b(x-2)(b-1) |
 如图,在平行四边形ABCD中,BC=12,CD=8,BE为∠ABC的平分线交AD于点E,则DE=4.
如图,在平行四边形ABCD中,BC=12,CD=8,BE为∠ABC的平分线交AD于点E,则DE=4.