题目内容
18．
如图，在平行四边形ABCD中，BC=12，CD=8，BE为∠ABC的平分线交AD于点E，则DE=4．
分析 根据四边形ABCD为平行四边形可得AE∥BC，根据平行线的性质和角平分线的性质可得出∠ABE=∠AEB，继而可得AB=AE，然后根据已知可求得DE的长度．
解答 解：∵四边形ABCD为平行四边形，
∴AE∥BC，AB=CD=12，
∴∠AEB=∠EBC，
∵BE平分∠ABC，
∴∠ABE=∠EBC，
∴∠ABE=∠AEB，
∴AB=AE，
∵BC=12，
∴DE=AD-AE=12-8=4，
故答案为：4．
点评 本题考查了平行四边形的性质，解答本题的关键是根据平行线的性质和角平分线的性质得出∠ABE=∠AEB．
练习册系列答案
相关题目
如图，在△ABC中，EF⊥AB，CD⊥AB．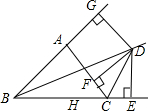
如图，已知BD是∠ABC的内角平分线，CD是∠ACB的外角平分线，由D出发，作点D到BC、AC和AB的垂线DE、DF和DG，垂足分别为E、F、G，则DE、DF、DG的关系是DE=DF=DG．
3．下列式子一定是最简二次根式的是（ ）
| A． | $\sqrt{12}$ | B． | $\sqrt{\frac{1}{2}}$ | C． | $\sqrt{2}$ | D． | $\sqrt{18}$ |
10．已知ma+b•ma-b=m12，则a的值为（ ）
| A． | 1 | B． | 4 | C． | 5 | D． | 6 |