题目内容
4．
如图，∠ABC=140°，D为圆上一点，则∠ADC的度数为140°或40°．
分析 由点A、B、C、D在圆上，利用圆周角定理及圆内接四边形的性质结合∠ABC=140°，即可得出∠ADC的度数，此题得解．
解答 解：∵点A、B、C、D在圆上，且∠ABC=140°，
∴∠ADC=∠ABC或∠ADC+∠ABC=180°，
∴∠ADC=140°或40°．
故答案为：140°或40°；
点评 本题考查了圆周角定理以及圆内接四边形的性质，根据圆周角定理及圆内接四边形的性质找出∠ADC=∠ABC或∠ADC+∠ABC=180°是解题的关键．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
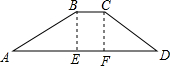如图，水库大坝的横截面是梯形，坝顶宽5米，坝高20米，斜坡AB的坡比为1：2.5，斜坡CD的坡比为1：2，求大坝的截面面积．
7．如果abcd＜0，则a+b=0，cd＞0，那么这四个数中负因数的个数至少有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |