题目内容
7.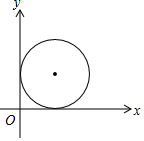 如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2017圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为( )
如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2017圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为( )| A. | (2018,1) | B. | (4034π+1,1) | C. | (2017,1) | D. | (4034π-1,1) |
分析 利用切线的性质可判定开始时该圆的圆心坐标为(1,1),在圆向右滚动时纵坐标不变,当该圆向x轴正方向滚动2017圈后,横坐标增加2017×2π,从而得到该圆向x轴正方向滚动2017圈后的圆心坐标.
解答 解:∵半径为1的圆,与两坐标轴相切,
∴开始时该圆的圆心坐标为(1,1),
∵圆的周长为2π,
∴该圆向x轴正方向滚动2017圈,
∴圆心的横坐标为1+2π×2017,纵坐标为1,
即该圆的圆心坐标为(4034π+1,1).
故选B.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
17.一个不透明的口袋中有6个白球和12个黑球,“任意摸出n个球,其中至少有一个白球”是必然事件,n等于( )
| A. | 6 | B. | 7 | C. | 13 | D. | 18 |
15.下列运算正确的是:( )
| A. | (a-b)2=a2-b2 | B. | a10÷a2=a5 | C. | (2a2b3)3=8a6b9 | D. | 2a2•3a3=6a6 |
12.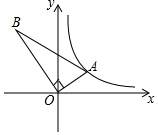 如图所示,在Rt△AOB中,∠AOB=90°,2OB=3OA,点A在反比例函数y=$\frac{2}{x}$的图象上,若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )
如图所示,在Rt△AOB中,∠AOB=90°,2OB=3OA,点A在反比例函数y=$\frac{2}{x}$的图象上,若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )
 如图所示,在Rt△AOB中,∠AOB=90°,2OB=3OA,点A在反比例函数y=$\frac{2}{x}$的图象上,若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )
如图所示,在Rt△AOB中,∠AOB=90°,2OB=3OA,点A在反比例函数y=$\frac{2}{x}$的图象上,若点B在反比例函数y=$\frac{k}{x}$的图象上,则k的值为( )| A. | 3 | B. | -3 | C. | -$\frac{9}{2}$ | D. | -$\frac{9}{4}$ |
19.2016年我国就业形势总体稳定,超过全年预期目标,成为经济运行的一大亮点,城镇新增就业1312万人,这个数据用科学记数法可以表示为( )
| A. | 1.312×106人 | B. | 1.312×107人 | C. | 13.12×106人 | D. | 0.1312×108人 |
17.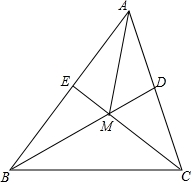 如图,已知(1)已知△ABC的两条中线BD、CE交于点M,A、D、M、E四点共圆,BC=8,则AM的长为( )
如图,已知(1)已知△ABC的两条中线BD、CE交于点M,A、D、M、E四点共圆,BC=8,则AM的长为( )
 如图,已知(1)已知△ABC的两条中线BD、CE交于点M,A、D、M、E四点共圆,BC=8,则AM的长为( )
如图,已知(1)已知△ABC的两条中线BD、CE交于点M,A、D、M、E四点共圆,BC=8,则AM的长为( )| A. | 2$\sqrt{3}$ | B. | $\frac{2}{3}$$\sqrt{3}$ | C. | $\frac{8}{3}$$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
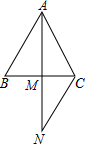 在△ABC中,AB=AC,过点C作CN∥AB且CN=AC,连接AN交BC于点M.求证:BM=CM.
在△ABC中,AB=AC,过点C作CN∥AB且CN=AC,连接AN交BC于点M.求证:BM=CM.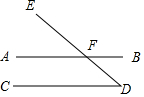 如图,∠D=49°,∠BFE=131°,试用三种不同的方法说明AB∥CD.
如图,∠D=49°,∠BFE=131°,试用三种不同的方法说明AB∥CD. 如图,小东在教学楼距地面8米高的窗口C处,测得正前方旗杆顶端A的仰角为55°,旗杆底部B的俯角为45°,求旗杆AB的高.(结果精确到0.1米)
如图,小东在教学楼距地面8米高的窗口C处,测得正前方旗杆顶端A的仰角为55°,旗杆底部B的俯角为45°,求旗杆AB的高.(结果精确到0.1米)