题目内容
18.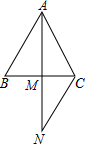 在△ABC中,AB=AC,过点C作CN∥AB且CN=AC,连接AN交BC于点M.求证:BM=CM.
在△ABC中,AB=AC,过点C作CN∥AB且CN=AC,连接AN交BC于点M.求证:BM=CM.
分析 根据等腰三角形的三线合一即可证明.
解答 证明:∵AB=AC,CN=AC,
∴AB=CN,∠N=∠CAN
又∵AB∥CN,
∴∠BAM=∠N,
∴∠BAM=∠CAM,
∴AM为∠BAC的平分线,
又∵AB=AC,
∴AM为三角形ABC的边BC上的中线,
∴BM=CM.
点评 本题主要考查了等腰三角形的性质以及平行线的性质,解题的关键是掌握平行线的性质以及三角形中线的知识,此题难度不大.

练习册系列答案
相关题目
9.在(-1)2017,(-3)0,$\sqrt{9}$,($\frac{1}{2}$)-2,这四个数中,最大的数是( )
| A. | (-1)2017 | B. | (-3)0 | C. | $\sqrt{9}$ | D. | ($\frac{1}{2}$)-2 |
6. 如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:(1)b2-4ac>0;(2)c>1;(3)b<0;(4)a+b+c<0.你认为其中错误的有( )
如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:(1)b2-4ac>0;(2)c>1;(3)b<0;(4)a+b+c<0.你认为其中错误的有( )
 如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:(1)b2-4ac>0;(2)c>1;(3)b<0;(4)a+b+c<0.你认为其中错误的有( )
如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:(1)b2-4ac>0;(2)c>1;(3)b<0;(4)a+b+c<0.你认为其中错误的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 1个 |
13.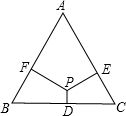 如图,P为等腰△ABC内一点,过点P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F,已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3,则AP的长为( )
如图,P为等腰△ABC内一点,过点P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F,已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3,则AP的长为( )
 如图,P为等腰△ABC内一点,过点P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F,已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3,则AP的长为( )
如图,P为等腰△ABC内一点,过点P分别作三条边BC、CA、AB的垂线,垂足分别为D、E、F,已知AB=AC=10,BC=12,且PD:PE:PF=1:3:3,则AP的长为( )| A. | $\frac{4}{3}$ | B. | $\frac{20}{3}$ | C. | 7 | D. | 8 |
3.若x=0是关于x的一元二次方程(a+2)x2-$\sqrt{a-2}$x+a2+a-6=0的一个根,则a的值是( )
| A. | a≠-2 | B. | a=2 | C. | a=-3 | D. | a=-3或a=2 |
7.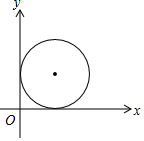 如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2017圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为( )
如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2017圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为( )
 如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2017圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为( )
如图,在平面直角坐标系中,放置半径为1的圆,与两坐标轴相切,若该圆向x轴正方向滚动2017圈后(滚动时在x轴上不滑动),则该圆的圆心坐标为( )| A. | (2018,1) | B. | (4034π+1,1) | C. | (2017,1) | D. | (4034π-1,1) |

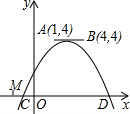 如图,点A,B的坐标分别为(1,4)和(4,4),将抛物线y=a(x-m)2+n平移并保持顶点在线段AB上,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则当点D的横坐标达到最大值时抛物线的解析式为y=-$\frac{1}{4}$(x-4)2+4.
如图,点A,B的坐标分别为(1,4)和(4,4),将抛物线y=a(x-m)2+n平移并保持顶点在线段AB上,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则当点D的横坐标达到最大值时抛物线的解析式为y=-$\frac{1}{4}$(x-4)2+4. 在图中涂黑一个小正方形,使得图中黑色的正方形成为轴对称图形,这样的小正方形可以有3个.
在图中涂黑一个小正方形,使得图中黑色的正方形成为轴对称图形,这样的小正方形可以有3个.