题目内容
5.已知二次函数y=-$\frac{1}{2}$x2+x+$\frac{3}{2}$.(1)用配方法将此二次函数化为顶点式;
(2)求出它的顶点坐标和对称轴方程.
分析 (1)利用配方法将二次函数的一般式变形为顶点式,此题得解;
(2)根据二次函数的顶点式,结合二次函数的性质即可得出顶点坐标以及对称轴.
解答 解:(1)二次函数y=-$\frac{1}{2}$x2+x+$\frac{3}{2}$=-$\frac{1}{2}$(x-1)2+2;
(2)∵二次函数y=-$\frac{1}{2}$(x-1)2+2,
∴二次函数的顶点坐标为(1,2),抛物线的对称轴为x=1.
点评 本题考查了二次函数的三种形式以及二次函数的性质,利用配方法将二次函数的一般式变形为顶点式是解题的关键.

练习册系列答案
相关题目
13.下列多项式:(1)x3+xy-y2;(2)-x2+2xy-y2;(3)xy+x2+y2;(4)1-x+$\frac{{x}^{2}}{4}$中,能用完全平方公式分解因式的是( )
| A. | (1)(2) | B. | (1)(3) | C. | (1)(4) | D. | (2)(4) |
20.$\frac{2•tan30°}{1-ta{n}^{2}30°}$的值等于( )
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{-\sqrt{3}}{3}$ |
17.已知2x2+y=1,x2-xy=2,则3x2+y(1-x)-1=( )
| A. | 4 | B. | -1 | C. | 3 | D. | 2 |
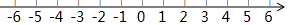 在数轴上画出表示下列各数的点,并用“<”号将这些数按从小到大的顺序连接起来:
在数轴上画出表示下列各数的点,并用“<”号将这些数按从小到大的顺序连接起来: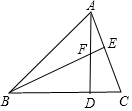 如图,△ABC的两条高线AD、BE交于点F,∠BAD=45°,∠C=60°,则∠BFD的度数为60°.
如图,△ABC的两条高线AD、BE交于点F,∠BAD=45°,∠C=60°,则∠BFD的度数为60°.