题目内容
6.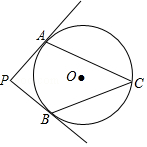 如图,PA、PB分别切⊙O于点A、B,点C在⊙O上,且∠ACB=54°,则∠P=72°.
如图,PA、PB分别切⊙O于点A、B,点C在⊙O上,且∠ACB=54°,则∠P=72°.
分析 连结OA、OB,如图,先根据切线的性质得OA⊥PA,OB⊥PB,则根据四边形内角和得到∠P+∠AOB=180°,再利用圆周角定理得到∠AOB=2∠ACB=108°,然后计算180°-∠AOB即可.
解答 解:连结OA、OB,如图,
∵PA、PB分别切⊙O于点A、B,
∴OA⊥PA,OB⊥PB,
∴∠P+∠AOB=180°,
∵∠AOB=2∠ACB=2×54°=108°,
∴∠P=180°-108°=72°.
故答案为72.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.

练习册系列答案
相关题目
16.点A(-3,2)关于x轴对称的点是B,点B关于y轴对称的点是C,则点C的坐标是( )
| A. | (-3,2) | B. | (3,2) | C. | (-3,-2) | D. | (3,-2) |
1.对于y=-2(x-3)2+2的图象下列叙述正确的是( )
| A. | 顶点作标为(-3,2) | B. | 对称轴为:直线x=-3 | ||
| C. | 当x≥3时y随x增大而减小 | D. | 函数的最小值是2 |
18.计算$\frac{1}{1×20}$+$\frac{1}{2×19}$+$\frac{1}{3×18}$+…+$\frac{1}{20×1}$-$\frac{20}{21}$($\frac{1}{1×19}$+$\frac{1}{2×18}$+…+$\frac{1}{19×1}$)的结果为( )
| A. | $\frac{1}{210}$ | B. | $\frac{1}{231}$ | C. | $\frac{1}{190}$ | D. | $\frac{1}{171}$ |
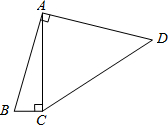 如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是什么?
如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是什么?
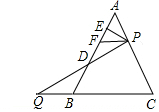 如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点.与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D,过P作PF∥BC.
如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一动点.与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D,过P作PF∥BC.