题目内容
 已知:如图,四边形ABCD为平行四边形,以CD为直径作⊙O,⊙O与边BC相交于点F,⊙O的切线DE与边AB相交于点E,且AE=3EB.
已知:如图,四边形ABCD为平行四边形,以CD为直径作⊙O,⊙O与边BC相交于点F,⊙O的切线DE与边AB相交于点E,且AE=3EB.(1)求证:△ADE∽△CDF;
(2)当CF:FB=1:2时,求⊙O与?ABCD的面积之比.
考点:切线的性质,勾股定理,平行四边形的性质,相似三角形的判定与性质
专题:几何综合题
分析:(1)根据平行四边形的性质得出∠A=∠C,AD∥BC,求出∠ADE=∠CDF,根据相似三角形的判定推出即可;
(2)设CF=x,FB=2x,则BC=3x,设EB=y,则AE=3y,AB=4y,根据相似得出
=
,求出x=2y,由勾股定理得求出DF=2
y,分别求出⊙O的面积和四边形ABCD的面积,即可求出答案.
(2)设CF=x,FB=2x,则BC=3x,设EB=y,则AE=3y,AB=4y,根据相似得出
| 3y |
| 3x |
| x |
| 4y |
| 3 |
解答:(1)证明:∵CD是⊙O的直径,
∴∠DFC=90°,
∵四边形ABCD是平行四边形,
∴∠A=∠C,AD∥BC,AB∥CD,
∴∠ADF=∠DFC=90°,
∵DE为⊙O的切线,
∴DE⊥DC,
∴DE⊥AB,
∴∠DEA=∠DFC=90°,
∵∠A=∠C,
∴△ADE∽△CDF;
(2)解:∵CF:FB=1:2,
∴设CF=x,FB=2x,则BC=3x,
∵AE=3EB,
∴设EB=y,则AE=3y,AB=4y,
∵四边形ABCD是平行四边形,
∴AD=BC=3x,AB=DC=4y,
∵△ADE∽△CDF,
∴
=
,
∴
=
,
∵x、y均为正数,
∴x=2y,
∴BC=6y,CF=2y,
在Rt△DFC中,∠DFC=90°,
由勾股定理得:DF=
=
=2
y,
∴⊙O的面积为π•(
DC)2=
π•DC2=
π(4y)2=4πy2,
四边形ABCD的面积为BC•DF=6y•2
y=12
y2,
∴⊙O与四边形ABCD的面积之比为4πy2:12
y2=π:3
.
∴∠DFC=90°,
∵四边形ABCD是平行四边形,
∴∠A=∠C,AD∥BC,AB∥CD,
∴∠ADF=∠DFC=90°,
∵DE为⊙O的切线,
∴DE⊥DC,
∴DE⊥AB,
∴∠DEA=∠DFC=90°,
∵∠A=∠C,
∴△ADE∽△CDF;
(2)解:∵CF:FB=1:2,

∴设CF=x,FB=2x,则BC=3x,
∵AE=3EB,
∴设EB=y,则AE=3y,AB=4y,
∵四边形ABCD是平行四边形,
∴AD=BC=3x,AB=DC=4y,
∵△ADE∽△CDF,
∴
| AE |
| AD |
| CF |
| CD |
∴
| 3y |
| 3x |
| x |
| 4y |
∵x、y均为正数,
∴x=2y,
∴BC=6y,CF=2y,
在Rt△DFC中,∠DFC=90°,
由勾股定理得:DF=
| DC2-FC2 |
| (4y)2-(2y)2 |
| 3 |
∴⊙O的面积为π•(
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
四边形ABCD的面积为BC•DF=6y•2
| 3 |
| 3 |
∴⊙O与四边形ABCD的面积之比为4πy2:12
| 3 |
| 3 |
点评:本题考查了平行四边形的性质,相似三角形的性质和判定,勾股定理的应用,主要考查学生综合运用性质进行推理和计算的能力.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 徐州市泉山区四中学生组织公益活动,有小学生、初中生、高中生和大学生参加,共1000人.各类学生人数比例见扇形统计图.
徐州市泉山区四中学生组织公益活动,有小学生、初中生、高中生和大学生参加,共1000人.各类学生人数比例见扇形统计图. 如图,已知⊙O中直径AB与弦AC的夹角为30°,过点C作⊙O的切线交AB的延长线于点D,OD=30cm.求:直径AB的长.
如图,已知⊙O中直径AB与弦AC的夹角为30°,过点C作⊙O的切线交AB的延长线于点D,OD=30cm.求:直径AB的长.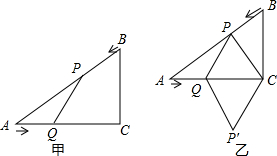 如图甲,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm.如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为t(s)(0<t<4),解答下列问题:
如图甲,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm.如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为t(s)(0<t<4),解答下列问题: 如图,直线y=kx+b经过A(-1,1)和B(-3,0)两点,则关于x的不等式组0<kx+b<-x的解集为
如图,直线y=kx+b经过A(-1,1)和B(-3,0)两点,则关于x的不等式组0<kx+b<-x的解集为 如图,水平放置的长方体的底面是边长为3和5的长方形,它的左视图的面积为12,则长方体的体积等于
如图,水平放置的长方体的底面是边长为3和5的长方形,它的左视图的面积为12,则长方体的体积等于