题目内容
 如图,OA⊥OB,OC⊥OD,∠AOE=∠COE,求证:OE平分∠BOD.
如图,OA⊥OB,OC⊥OD,∠AOE=∠COE,求证:OE平分∠BOD.考点:垂线,角平分线的定义
专题:证明题
分析:先求出∠AOD=∠BOC,再求出∠DOE=∠BOE,即可得出结论.
解答:证明:∵OA⊥OB,OC⊥OD,
∴∠AOB=∠COD=90°,
∴∠AOD=∠BOC,
∵∠AOE=∠COE,
∴∠AOD+∠AOE=∠BOC+∠COE,
即∠DOE=∠BOE,
∴OE平分∠BOD.
∴∠AOB=∠COD=90°,
∴∠AOD=∠BOC,
∵∠AOE=∠COE,
∴∠AOD+∠AOE=∠BOC+∠COE,
即∠DOE=∠BOE,
∴OE平分∠BOD.
点评:本题考查了垂线和角平分线的定义;弄清几组角之间的等量关系,证出∠DOE=∠BOE是解决问题的关键.

练习册系列答案
相关题目
下列事件:①在足球赛中,弱队战胜强队.②抛掷一枚硬币,硬币落地时正面朝上.③任取两个整数,其和大于1.④长为3cm,5cm,9cm的三条线段能围成一个三角形.其中随机事件有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
由若干个相同的小立方体搭成的几何体的三视图如图所示,则搭成这个几何体的小立方体的个数是( )


| A、3 | B、4 | C、5 | D、6 |
 已知ABCD为正方形,E、F分别是AD、CD上的一点,∠EBF=45°,△EFD周长为2,求正方形边长.
已知ABCD为正方形,E、F分别是AD、CD上的一点,∠EBF=45°,△EFD周长为2,求正方形边长. 2013年开始,国家在113个环境保护重点城市和国家环境保护模仿城市开展PM2.5的检测工作并发布检测信息.“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物.某日随机抽取25个城市检测点的研究性数据,并绘制成统计表和扇形统计图如下:
2013年开始,国家在113个环境保护重点城市和国家环境保护模仿城市开展PM2.5的检测工作并发布检测信息.“PM2.5”是指大气中危害健康的直径小于或等于2.5微米的颗粒物.某日随机抽取25个城市检测点的研究性数据,并绘制成统计表和扇形统计图如下: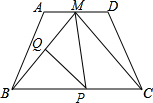 如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,BC=8,MB=5
如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,BC=8,MB=5 如图,OA=OC,已知tan∠AOC=
如图,OA=OC,已知tan∠AOC= 如图,在Rt△ABC中,∠C=90°,AC=2,BC=1,则cosA的值是
如图,在Rt△ABC中,∠C=90°,AC=2,BC=1,则cosA的值是