题目内容
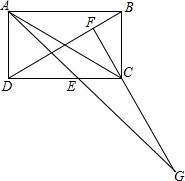 如图,矩形ABCD中,过C作CF⊥BD于F,延长FC至G,CG=BD,连AG交CD于E,∠AED的度数是多少?
如图,矩形ABCD中,过C作CF⊥BD于F,延长FC至G,CG=BD,连AG交CD于E,∠AED的度数是多少?考点:矩形的性质
专题:
分析:过A点作AM⊥BD,根据已知条件求出∠G=∠MAE,再根据矩形的性质得出CG=AC,求出∠G=∠CAE,得出∠CAE=∠MAE,再根据∠AOD+∠MAO=90°,得出2∠OCD+2∠EAC=90°,从而求出∠AED的度数.
解答: 解:过A点作AM⊥BD,
解:过A点作AM⊥BD,
∵CF⊥BD,
∴CF∥AM,
∴∠G=∠MAE,
∵四边形ABCD为矩形,
∴AC=BD,OC=OD,∠OCD=∠ODC,
∵CG=BD,
∴CG=AC,
∴∠G=∠CAE,
∴∠CAE=∠MAE,
∵∠AOD+∠MAO=90°,
∴2∠OCD+2∠EAC=90°,
∴∠OCD+∠EAC=45°,
∴∠AED=45°.
 解:过A点作AM⊥BD,
解:过A点作AM⊥BD,∵CF⊥BD,
∴CF∥AM,
∴∠G=∠MAE,
∵四边形ABCD为矩形,
∴AC=BD,OC=OD,∠OCD=∠ODC,
∵CG=BD,
∴CG=AC,
∴∠G=∠CAE,
∴∠CAE=∠MAE,
∵∠AOD+∠MAO=90°,
∴2∠OCD+2∠EAC=90°,
∴∠OCD+∠EAC=45°,
∴∠AED=45°.
点评:此题考查了矩形的性质,用到的知识点是平行线的性质、矩形的性质,关键是根据题意作出辅助线,找出相应的对应关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在平面直角坐标系中,直线y=kx+4过点(-3,-5),且与x轴、y轴分别交于A,B两点,求不等式kx+4≤0的解集.
在平面直角坐标系中,直线y=kx+4过点(-3,-5),且与x轴、y轴分别交于A,B两点,求不等式kx+4≤0的解集. 如图,在Rt△ABC中,已知∠B=90°,∠C=30°,点D是BC的中点,求sin∠DAC.
如图,在Rt△ABC中,已知∠B=90°,∠C=30°,点D是BC的中点,求sin∠DAC. 已知,如图,AB∥DC,AC、BD交于O,且AC=BD,求证:OD=OC.
已知,如图,AB∥DC,AC、BD交于O,且AC=BD,求证:OD=OC. 如图,在菱形ABCD中,DE⊥AB,cosA=
如图,在菱形ABCD中,DE⊥AB,cosA= 已知ABCD为正方形,E、F分别是AD、CD上的一点,∠EBF=45°,△EFD周长为2,求正方形边长.
已知ABCD为正方形,E、F分别是AD、CD上的一点,∠EBF=45°,△EFD周长为2,求正方形边长.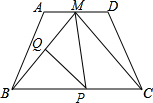 如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,BC=8,MB=5
如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,BC=8,MB=5