题目内容
 如图,在平面直角坐标系xOy中,点P(a,b)在第一象限.以P为圆心的圆经过原点,与y轴的另一个交点为A.点Q是线段OA上的点(不与O,A重合),过点Q作PQ的垂线交⊙P于点B(m,n),其中m≥0.
如图,在平面直角坐标系xOy中,点P(a,b)在第一象限.以P为圆心的圆经过原点,与y轴的另一个交点为A.点Q是线段OA上的点(不与O,A重合),过点Q作PQ的垂线交⊙P于点B(m,n),其中m≥0.(1)若b=5,则点A坐标是
(2)在(1)的条件下,若OQ=8,求线段BQ的长;
(3)若点P在函数y=x2(x>0)的图象上,且△BQP是等腰三角形.
①直接写出实数a的取值范围:
②在
| 1 |
| 2 |
| ||
| 4 |
| 10 |
考点:圆的综合题
专题:
分析:(1)过点P作PH⊥OA于点H,由垂径定理可求出OA的长,进而可求出A的坐标;
(2)连接BP、OP,由已知条件易求QH,在Rt△QHP中,由勾股定理可得:PQ2=QH2+PH2=9+PH2,在RtPHO中,由勾股定理可得:PO2=OH2+PH2=25+PH2=BP2,
进而在RtBQP中,BQ2=BP2-PQ2=(25+PH2)-(9+PH2)=16.所以BQ=4;
(3)①把P点的坐标代入抛物线解析式可得到b=a2,进而可求出a≥1;②在
,
,
这三个数中,线段PQ的长度可以为
,作BM⊥y轴于点M,首先求出a=2,再求出MQ=PH=2,利用勾股定理可求出MB=QH=
=
.所以可得:B1(
,6+
),若点Q在OH上,再由抛物线对称性可得B2(
,2-
)综上,当PQ=
时,B点坐标为(
,6+
)或(
,2-
).
(2)连接BP、OP,由已知条件易求QH,在Rt△QHP中,由勾股定理可得:PQ2=QH2+PH2=9+PH2,在RtPHO中,由勾股定理可得:PO2=OH2+PH2=25+PH2=BP2,
进而在RtBQP中,BQ2=BP2-PQ2=(25+PH2)-(9+PH2)=16.所以BQ=4;
(3)①把P点的坐标代入抛物线解析式可得到b=a2,进而可求出a≥1;②在
| 1 |
| 2 |
| ||
| 4 |
| 10 |
| 10 |
| PQ2-PH2 |
| 6 |
| 6 |
| 6 |
| 6 |
| 6 |
| 10 |
| 6 |
| 6 |
| 6 |
| 6 |
解答:解:(1)过点P作PH⊥OA于点H,
∴OA=2OH,
∵b=5,
∴OH=5,
∴OA=10,
∴点A坐标是(0,10).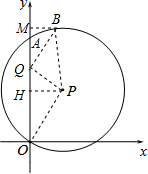
故答案为:(0,10).
(2)连接BP、OP.
∵b=5,PH⊥OA,
∴OH=AH=5.
∵OQ=8,
∴QH=OQ-OH=3.
在Rt△QHP中,PQ2=QH2+PH2=9+PH2,
在RtPHO中,PO2=OH2+PH2=25+PH2=BP2,
在RtBQP中,BQ2=BP2-PQ2=(25+PH2)-(9+PH2)=16.
∴BQ=4.
(3)①∵点P在函数y=x2(x>0)的图象上,
∴b=a2,
∴a≥1,
故答案为:a≥1;
②在
,
,
这三个数中,线段PQ的长度可以为
,
理由如下:
∵△BQP是等腰直角三角形,PQ=
,
∴半径BP=2
.
又∵P(a,a2),
∴OP2=a2+a4=(2
)2.
即a4+a2-20=0.
解得a=±2.
∵a>0
∴a=2.
∴P(2,4).
如图,作BM⊥y轴于点M,则△QBM≌△PQH.
∴MQ=PH=2,
∴MB=QH=
=
.
∴B1(
,6+
).
若点Q在OH上,由对称性可得B2(
,2-
)
综上,当PQ=
时,B点坐标为(
,6+
)或(
,2-
).
∴OA=2OH,
∵b=5,
∴OH=5,
∴OA=10,
∴点A坐标是(0,10).

故答案为:(0,10).
(2)连接BP、OP.
∵b=5,PH⊥OA,
∴OH=AH=5.
∵OQ=8,
∴QH=OQ-OH=3.
在Rt△QHP中,PQ2=QH2+PH2=9+PH2,
在RtPHO中,PO2=OH2+PH2=25+PH2=BP2,
在RtBQP中,BQ2=BP2-PQ2=(25+PH2)-(9+PH2)=16.
∴BQ=4.
(3)①∵点P在函数y=x2(x>0)的图象上,
∴b=a2,
∴a≥1,
故答案为:a≥1;
②在
| 1 |
| 2 |
| ||
| 4 |
| 10 |
| 10 |
理由如下:
∵△BQP是等腰直角三角形,PQ=
| 10 |
∴半径BP=2
| 5 |
又∵P(a,a2),
∴OP2=a2+a4=(2
| 5 |
即a4+a2-20=0.
解得a=±2.
∵a>0
∴a=2.
∴P(2,4).
如图,作BM⊥y轴于点M,则△QBM≌△PQH.
∴MQ=PH=2,
∴MB=QH=
| PQ2-PH2 |
| 6 |
∴B1(
| 6 |
| 6 |
若点Q在OH上,由对称性可得B2(
| 6 |
| 6 |
综上,当PQ=
| 10 |
| 6 |
| 6 |
| 6 |
| 6 |
点评:本题着重考查了待定系数法求二次函数解析式、勾股定理的运用,三角形全等、探究等腰三角形的构成情况等重要知识点,综合性强,能力要求极高.考查学生分类讨论,数形结合的数学思想方法.

练习册系列答案
相关题目
在Rt△ABC中,∠C=90°,sinA=
,则cosA的值等于( )
| 4 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,⊙O中的弦AB⊥弦CD,垂足为点P,OH⊥弦CD,垂足为点H,若PH=3,OH=2,则圆中阴影部分面积与其他部分面积的差是
如图,⊙O中的弦AB⊥弦CD,垂足为点P,OH⊥弦CD,垂足为点H,若PH=3,OH=2,则圆中阴影部分面积与其他部分面积的差是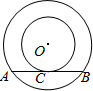 如图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于C.设弦AB的长为d,圆环的面积S与d之间有怎样的数量关系?
如图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于C.设弦AB的长为d,圆环的面积S与d之间有怎样的数量关系?