题目内容
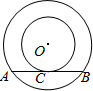如图，以O为圆心的两个同心圆中，大圆的弦AB切小圆于C．设弦AB的长为d，圆环的面积S与d之间有怎样的数量关系？考点：切线的性质,勾股定理,垂径定理
专题：
分析：首先利用切线的性质求出BC的长，再利用圆环面积求法得出答案．
解答：
解：S=π（OB2-CO2）=
，
理由：连接CO，
∵以O为圆心的两个同心圆中，大圆的弦AB切小圆于C，
∴CO⊥AB，
∵弦AB的长为d，
∴BC=
，
∴S=π（OB2-CO2）=
．
解：S=π（OB2-CO2）=| πd2 |
| 4 |
理由：连接CO，
∵以O为圆心的两个同心圆中，大圆的弦AB切小圆于C，
∴CO⊥AB，
∵弦AB的长为d，
∴BC=
| d |
| 2 |
∴S=π（OB2-CO2）=
| πd2 |
| 4 |
点评：此题主要考查了切线的性质以及勾股定理以及垂径定理，得出BC的长是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，图中共有
如图，在平面直角坐标系xOy中，点P（a，b）在第一象限．以P为圆心的圆经过原点，与y轴的另一个交点为A．点Q是线段OA上的点（不与O，A重合），过点Q作PQ的垂线交⊙P于点B（m，n），其中m≥0．下列关于概率的说法，正确的是（ ）
| A、天气预报说明天下雨的概率是50%，所以明天将有一半的时间在下雨 | ||
| B、某彩票中奖的概率是1%，买100张彩票一定会中奖 | ||
C、做投掷硬币试验时，每多投掷一次，正面朝上的频率就更接近于
| ||
| D、在同一年出生的367名学生中，至少有两人的生日是同一天 |
（-3x2）•（-
x3m•yn）（-ym）的结果是（ ）
| 2 |
| 3 |
| A、3x4mymn | ||
B、-
| ||
| C、-2x3m+2ym+n | ||
D、-
|
如图，在△ABC中，∠BAC=110°，AB，AC的垂直平分线分别交BC于点D，E，则∠DAE=